Reflections
What I Like. I think that the Diversity Choice Rule (which uses greedy merit-based selection to select among assignments that maximize diversity) is a reasonable approach. When f is ordinally concave, it is basically the only reasonable approach.
Even when f is not ordinally concave, the Diversity Choice Rule may be a reasonable solution. In fact, Carlos Bonet, Jay Sethuraman and I have a working paper which considers a special case of this model where
- each student is their own type,
- there is only one contract involving each student, and
- the diversity index is binary.
Carlos, Jay, and I argue that the Diversity Choice Rule is the only “explainable” policy (I won’t go into how we formalize this claim).
This paper could potentially help us answer questions that we have grappled with, like “What should the designer do if the contracts X make it impossible to satisfy their original diversity objective?” For example, suppose the designer may wish to accept a certain number of students of each gender. If not enough women apply, it seems natural that the designer should accept as many women as possible. This can be assured by using a non-binary diversity index.
What I Found Unsatisfying. My first reaction when reading this paper was “this is basically taking what we already know – that greedy selection works well when you have a matroid – and restating it using fancy and opaque terminology.” While I have softened a bit from this uncharitable reaction, it’s hard for me to tell how much of the math in this paper is new or innovative, and how much is just restating known results about matroids. (For what it’s worth, the same critique applies to some of the results in my work with Carlos and Jay.)
I do think that there is value to offering different ways to describe choice functions – especially if these descriptions align with how policymakers think about these issues. Using a “diversity index” may be natural in certain applications. However, if we truly want to take these ideas to practice, a key question that we must confront is, “what are reasonable choices for the diversity index?” There are essentially unlimited possibilities, and this question is almost completely ignored by the present paper.
The authors give several examples (Examples 2-4) of ordinally concave diversity indices, but these are presented very abstractly (devoid of any application). I would like to see a more thorough discussion of possible of diversity indices, including examples that are not ordinally concave, in addition to examples that are.
My suspicion is that many natural rules are not ordinally concave. For example, suppose that we are choosing two candidates to serve as representatives, and get one “diversity point” for each of the following that is true (i) at least one woman, (ii) at least one man, (iii) at least one person under 40, (iv) at least one person over 40. The Diversity Choice Rule with this f may choose a young woman and an old man ranked #1 and #10, respectively, when candidates #2 and #3 are an older woman and a young man and would also get a maximum score of 4.
If the designer’s preferred f is not ordinally concave, do the authors still recommend the Diversity Choice Rule? Something else? Or do they recommend changing f to make it ordinally concave?
What I Found Confusing. In this paper, the authors define what it means for a diversity index f to be
- ordinally concave (Definition 6),
- M-concave (Definition 10),
- M♮-concave (Definition 11),
- pseudo M♮-concave (Definition 8),
- pseudo M♮-concave+ (Definition 9),
- semi-strictly pseudo M♮-concave (Definition 12).
While they use a helpful running example (Example 1) to illustrate distinctions between some of these concepts, the sheer number of definitions, along with their similar and not-very-informative names, make these distinctions quite difficult to internalize. Figure 1 shows my attempts to map the relationship between these properties. Ordinal concavity is weaker than all of the other notions except pseudo-M♮ concavity.
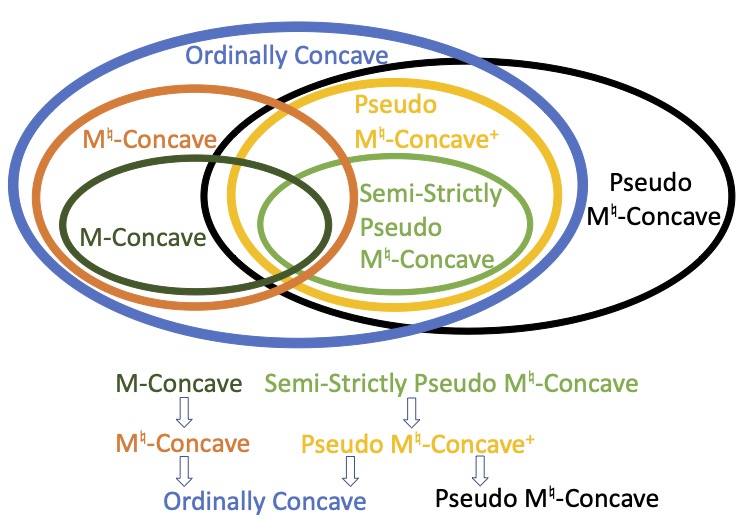
Figure 1: Relationships between concavity notions mentioned in the paper.
This reminds me of the literature on matching with contracts, where substitutability plays a key role in ensuring that deferred-acceptance-like algorithms have good properties. It turns out that slightly weaker notions suffice to ensure some or all of these properties, leading to papers introducing unilateral substitutability, bilateral substitutability, and substitutable completability.
To me, the presence of so many related but distinct conditions is a sign that our current understanding is incomplete. I hope that as our understanding evolves, we can simplify the web of concavity conditions above (none of which has been shown to be necessary to ensure nice properties) to a shorter and easier-to-digest list.