Model (Assumptions)

To analyze the situation without introducing too much complexity, I will make several assumptions.

• The Lions’ chance of kicking the field goal doesn’t depend on where the ball is spotted.
• The Packers’ chance of scoring in the final minute don’t depend on the exact place their drive starts.

I think these are both very reasonable assumptions, given that a 4th and inches play is likely to move the spot of the ball by at most a few yards. From here, I made a few more assumptions:

• The Lions will make the field goal.
• The Packers have no chance of scoring a touchdown in regulation (only a field goal).
• If the game goes to overtime, each team has a 50% chance of winning.
• The Lions’ probability of converting on 4th down is \(p_c\).
• The Packers’ probability of scoring a field goal if they get the ball back is \(p_s\).

All of the first three assumptions feel pretty reasonable to me.¹ In the code at the end of the post, I will allow for the possibility that the Lions miss the field goal.

Analysis

If the Lions kick the field goal, they win unless the Packers tie it and win in overtime. Thus, the Lions’ chances of winning if they choose to kick are \(1 - p_s/2\).

If the Lions go for it and make it, they will win: they run down the clock and kick the field goal as time expires. If they go for it and fail, then they need the Packers not to score in regulation, and to hope for an overtime win. Averaging these two scenarios, the Lions’ chance of winning if they go for it is \(p_c + (1-p_c)(1-p_s)/2\).

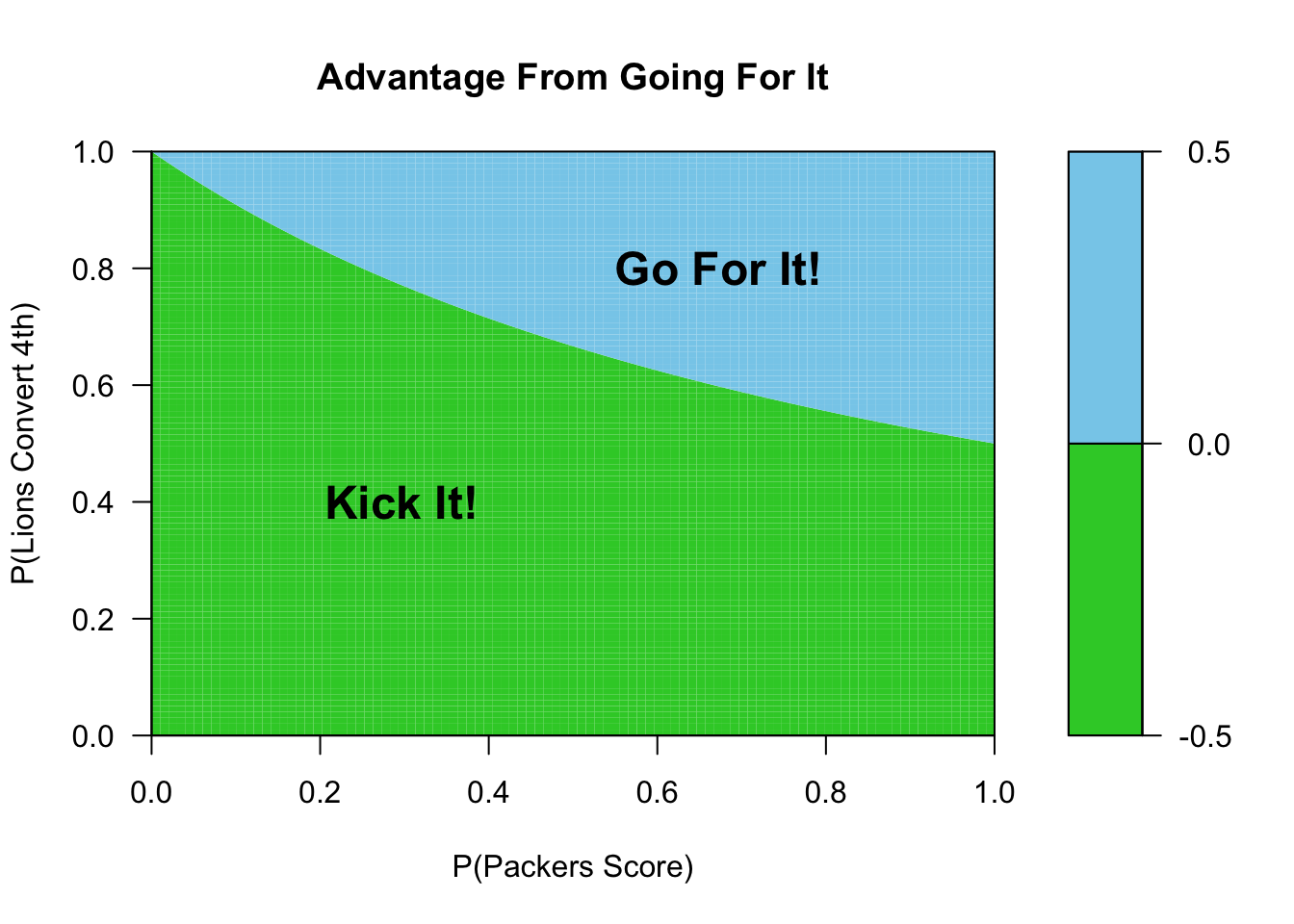
The right decision obviously depends on \(p_c\). If the Lions know they will convert, they should of course go for it. If they know they won’t convert, they should kick. For any value of \(p_s\), we can solve for the probability of converting that makes the two options equally good. This yields the equation \[p_c = 1/(1+p_s).\]

Putting this to work, if the Lions think the Packers have a \(p_s = 1/3\) chance of scoring, then they should go for 4th down so long as they think their chance of converting is at least \(1/(1+1/3) = 75\%\). If the Lions think the Packers’s chance of scoring is 50%, then they should go for 4th down as long as their chance of converting is at lest \(1/(1+1/2) = 2/3\).

We can visualize this using the following graph, which tells us what to do as a function of \(p_s\) and \(p_c\).

#f = probability that Lions make the field goal
#ps = probability that Packers score if they get the ball
#pc = probability that Lions convert on 4th down
win_prob_kick = function(ps,f){ return(f*(1-ps/2)+(1-f)*(1-ps)/2)}
win_prob_go = function(pc,ps,f){pc*f+pc*(1-f)/2+(1-pc)*(1-ps)/2}

#Function to create colorful graphs!
#h = function of x and y to be plotted
plot_heatmap = function(h, level_breaks,custom_palette){
  
  x_vals = y_vals = seq(0, 1, length.out = 100)
  filled.contour(
    x = x_vals,
    y = y_vals,
    z = outer(x_vals, y_vals,h),
    color.palette = function(n) custom_palette(n),
    levels = level_breaks,
    xlab = "P(Packers Score)", ylab = "P(Lions Convert 4th)", main = "Advantage From Going For It",
    key.axes = {
      axis(4, at = level_breaks, labels = format(level_breaks, digits = 2))
    }
  )
}

palette = colorRampPalette(c("limegreen", "white", "skyblue"))
f = 1 #Probability of making the field goal
#delta = gain in win probability from going for it
delta = function(ps,pc){win_prob_go(pc,ps,f)-win_prob_kick(ps,f)}

plot_heatmap(delta,level_breaks=c(-.5,0,.5),custom_palette=palette)
text(0.2, 0.4, "Kick It!", cex = 1.5, font = 2)
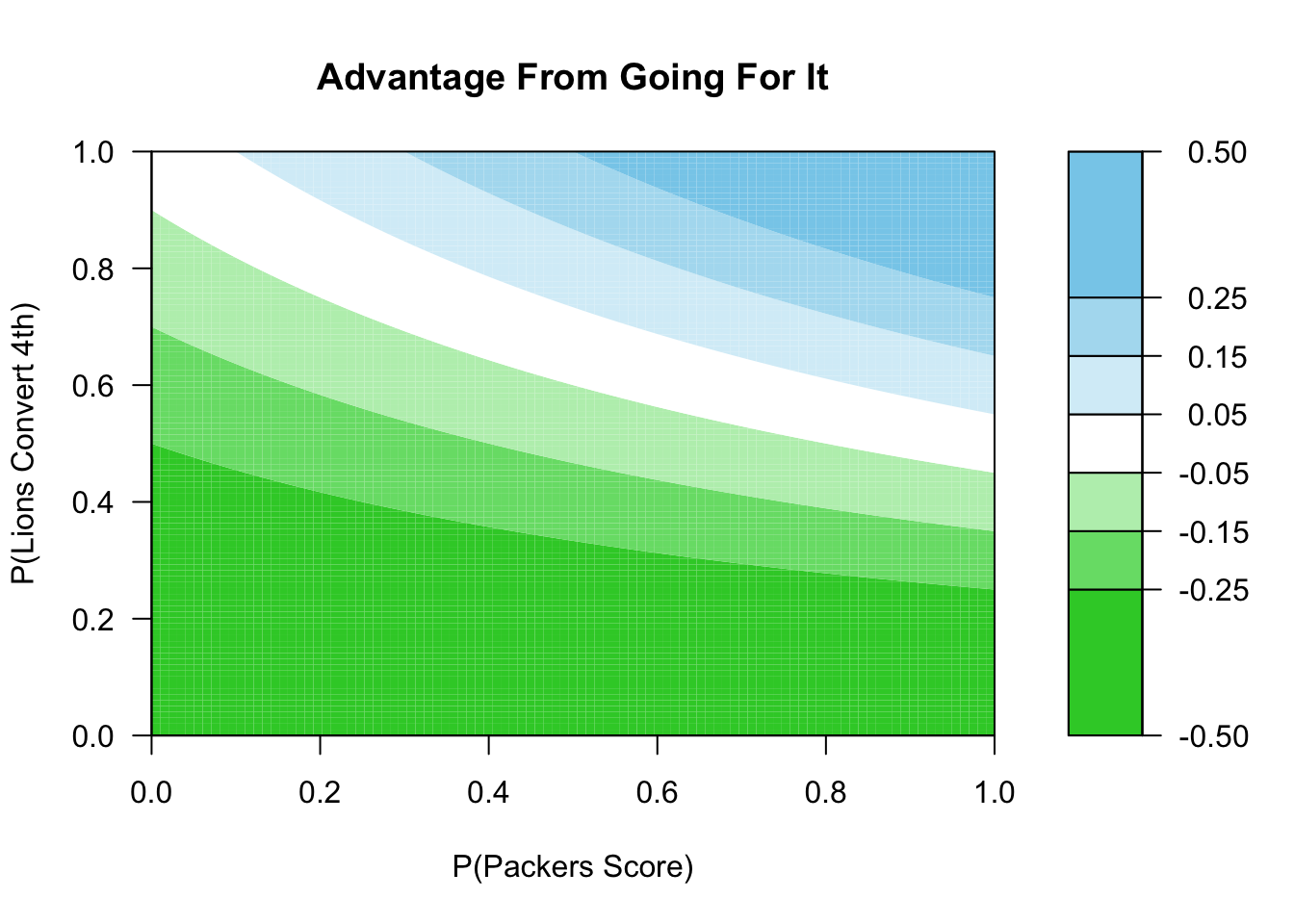
text(0.5, 0.8, "Go For It!",cex = 1.5, font = 2)

This graph tells us when to go for it, but not how much it matters. When is this a consequential decision? We can see this using the following graph. Dark blue means that it’s a much better decision to go for it (probability of winning increases by at least 25%), while dark green means that it’s much better to kick (going for it decreases probability of winning by at least 25%).

plot_heatmap(delta,level_breaks = c(-.5,-.25,-.15,-.05,.05,.15,.25,.5),custom_palette=palette)

So, what should the Lions have done? I would probably guestimate the Lions’ chance of converting at 75-80%. This means that going for it was the right call so long as the Packers’ chance of scoring a field goal was at least 25-30%. That sounds about right, suggesting to me that this was actually a fairly close call.

You might (reasonably) disagree with my ballpark estimates of \(p_s\) and \(p_c\). Based on your own estimates, use the chart above to see what the Lions should have done, and how much it mattered! By changing the value \(f\) in the code, you can produce analogous charts for cases where the Lions might miss the field goal.