Adaptive Investment

The preceding section establishes that among non-adaptive (“set it and forget it”) investment policies, there is no reason that the investment in stocks should decrease over time. Why, then, is this advice so prevalent?

One important observation is that I can adjust my behavior based on how my portfolio is doing. For example, I might initially invest in stocks, and then check my portfolio’s value several years later. If the portfolio has done well, I will shift my money to bonds, to lock in my savings. If the portfolio has tanked, shifting it to bonds will still leave me too poor to retire, so I keep my money in stocks and hope for good returns.³

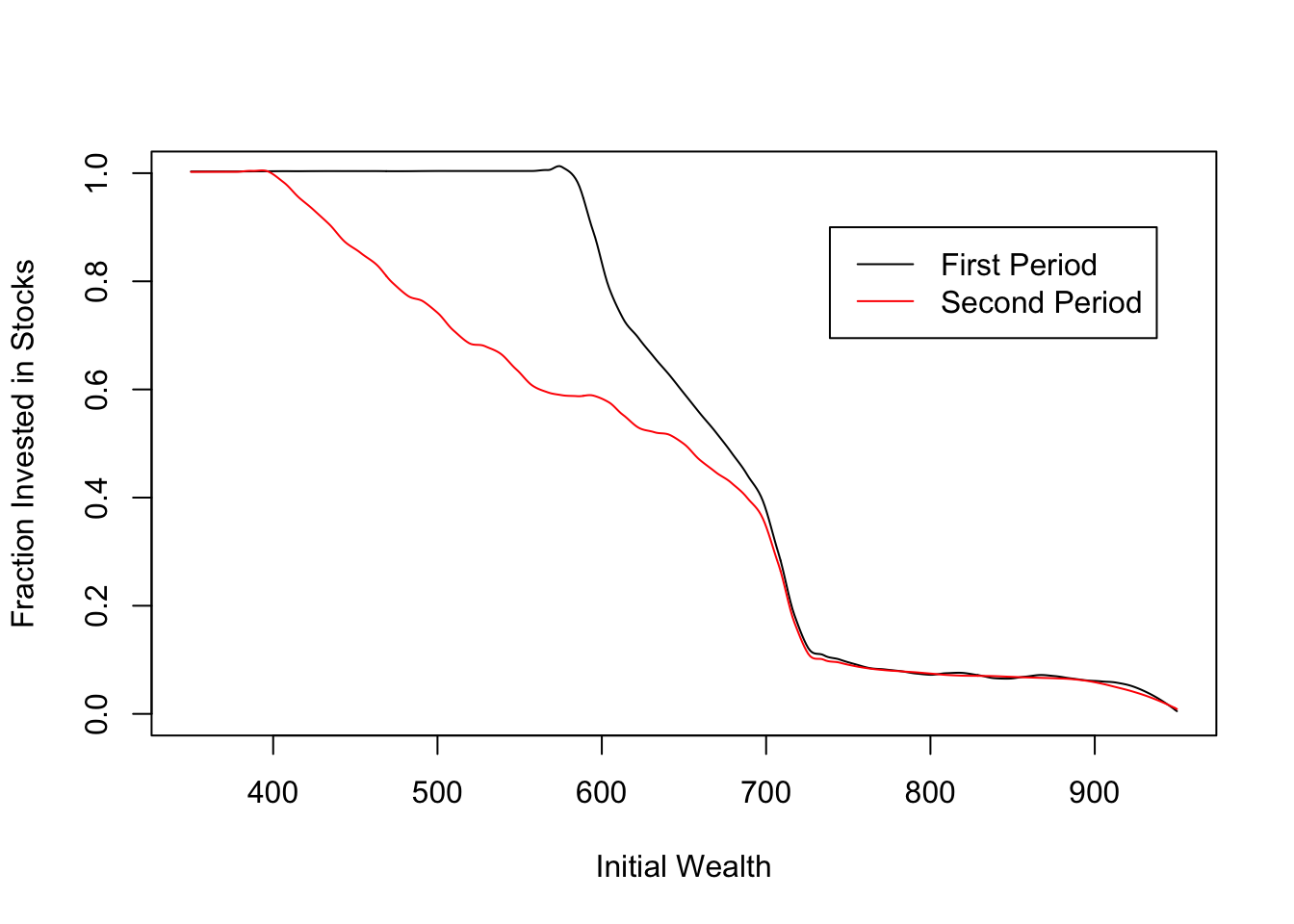
This suggests that the optimal strategy will start with risky assets, to resolve uncertainty early and be able to respond accordingly. We can test this intuition numerically using dynamic programming. The following code is for a two-period example.⁴ In this example, on average, the investor shifts money from stocks to bonds in the second period, but in some cases she actually does the reverse.⁵

#Given vectors X,Y such that X is increasing and Y = g(X), returns a discretized function approximating g
approximate = function(X,Y){
    return(Vectorize(function(x){
        i = max(c(which(X < x),1))
        return(Y[i]) #Could also do an average of Y[i] and Y[i+1], or linear interpolation  
    }))
}

#Given current wealth w, return from safe asset s, value function V and return from risky asset (r,p), computes expected utility from any given portfolio mix alpha
# p is a probability vector of the same length as r, and s and w are scalars.  
expectedUtility = function(w,s,r,p,V){
    return(Vectorize(function(alpha){
         return(sum(V((alpha*r+(1-alpha)*s)*w)*p))
    })) 
}

s = 1  #return from safe asset
r = .6 + c(0:10)/10  #possible returns from risky asset
p = rep(1/length(r),length(r)) #p[i] is probability of return r[i]


#Utility of wealth function

#U for plot 1
U = Vectorize(function(x){return(1/(1+exp(-a*(x-b))))})   

#Other possible utility functions
#U = Vectorize(function(x){return(sqrt(x/b)/2)})
#Target of 650
#U = Vectorize(function(x){if(x>=650) return(1); return(0)})

a = 0.02; b= 650;
N = 250
W = b+6*rep(-N:N)/(a*N)   #Different levels of wealth, in a range relevant to U

#Solving a two-period problem
T = 2

V = matrix(0,nrow = T+1,ncol=length(W)) #V[t+1,i] gives value of having W[i] dollars with t periods remaining
Alpha = matrix(0,nrow = T+1,ncol=length(W)) #Alpha[t+1,i] gives optimal portfolio wit W[i] dollars and t periods remaining
V[1,] = U(W)
for(t in 1:T){
    for(i in 1:length(W)){
        EU = expectedUtility(W[i],s,r,p,approximate(W,V[t,]))(c(0:N)/N)  #Taking this approach because the optimize function works poorly for locally flat functions
        V[t+1,i] = max(EU)
        Alpha[t+1,i] = which(EU==max(EU))[1]/N
        #soln = optimize(expectedUtility(W[i],s,r,p,approximate(W,V[t,])),interval=c(0,1),maximum=TRUE)
        #Alpha[t+1,i] = soln$maximum  #What is optimal alpha, given t remaining periods and wealth level W[i]?
        #V[t+1,i] = soln$objective #What is expected value, given t remaining periods and wealth level W[i]?
    }
}
#Two period model -- compare alpha in first period to average alpha in second period
AlphaSecondPdAvg = rep(0,length(W))  #AlphaSecondPdAvg[i] gives average alpha in second period, when investor has W[i] with two periods to go and behaves optimally
alphafn = approximate(W,Alpha[2,])  #alphafn(w) says what alpha to choose given wealth of w and one period remaining
for(i in 1:length(W)){
    AlphaSecondPdAvg[i] = sum(alphafn((Alpha[3,i]*r+(1-Alpha[3,i])*s)*W[i])*p)  #Alpha[3,i] is optimal alpha, given wealth W[i] with two periods remaining
}
plot(NULL,xlab='Initial Wealth',xlim=c(W[1],W[length(W)]),ylab='Fraction Invested in Stocks',ylim=c(0,1))
lines(W,predict(loess(Alpha[3,]~W,span=0.1)),col='black')
lines(W,predict(loess(AlphaSecondPdAvg~W,span=0.1)),col='red')
legend(x=W[N*1.3],y=0.9,legend = c('First Period','Second Period'),col=c('black','red'),lty=c(1,1))

Discussion

So, does it make sense to gradually shift assets from stocks to bonds as retirement approaches?

My answer is a qualified yes. An investor who actively manages her portfolio to prepare for retirement might reasonably expect to see the percentage of stocks decline over the years. The reason for this is that investing in stocks early provides information which can be used to make future decisions. In the model, the only decision is the mix of stocks and bonds, but in reality an investor may make other adjustments in response to early returns, such as changing consumption behavior or deciding to work for a few extra years.

However, the shift to bonds only happens on average, and only makes sense if the investor is looking at her retirement account and adjusting her behavior accordingly. This suggests that sales pitch for Target Date Funds doesn’t really make sense – they cater to investors who want to set aside money and forget about it until retirement, but adopt a “glide” strategy that can’t easily be justified for these investors.

As one Investopedia article states,

One retiree may have enough money on hand to invest strictly in bonds and other fixed-income securities. Another, requiring both growth and income, may need an equity component to keep the portfolio on track. A fund that meets the needs of one of these investors is unlikely to meet the needs of the other.

Will I redirect my contributions away from the Target Date Fund? Not right away – it’s mostly stocks right now, as it likely should be. But don’t be surprised if I end up shifting the money more actively at some point in the future.

Questions for readers: Is your money in a TDF? Why do you think these are so common? And what is the best counter-argument to the ideas above?