The Procedure

Here is the procedure: let \(B\) be the amount you are borrowing, \(R\) be your annual interest rate, and \(T\) the number of years that the loan will last.

The first step is to calculate your monthly payment without interest. This is easy: take the principal \(B\), and divide it by the total number of payments \(N = 12T\). So if you’re borrowing \(\$360,000\) over 30 years = 360 months, the monthly payment at a 0% interest rate would be \(\$1,000\).

So far, so good. But of course, your monthly payment will actually be much higher! We need to account for the interest that you will pay. To do this, we will multiply your interest-free monthly payment by some multiplier \(P > 1\), which is the amount you pay back for every \(\$1\) that you borrow.

We will estimate this quantity as follows: \[\hat{P} = 1 + \frac{RT}{2} + \frac{(RT)^2}{12}.\] For example, suppose that your \(T = 30\) year mortgage has an \(R = 5\%\) interest rate. Then \(RT = .05 \times 30 = 1.5\), and \(\hat{P} = 31/15 = 1.9375\). This says that for each dollar you borrow, you will eventually pay back approximately $1.94.

From this, we can calculate your monthly payment by simply multiplying \(\hat{P}\) by your interest-free payment. In other words, \[\hat{M} = \frac{B\hat{P}}{N} = \frac{B}{12T}\left(1+\frac{RT}{2} + \frac{(RT)^2}{12}\right).\] For our running example with a 30-year loan with 5% interest and principal of $360,000, this formula says that my monthly payment will be approximately $1,937.50. An online mortgage calculator gives us the exact answer of \(\$1,932.56\). Not bad!

Let’s say mortgage rates rise, to 7.5%. Now \(RT = 2.25\), so \(\hat{P} = 2.547\), meaning that you will now have to pay $2.547 for every dollar that you borrowed. Multiply this by \(B/N = 1000\), and we see that our monthly mortgage payment rises to $2,547. This is not far from the exact answer from an online calculator: $2,517.

We can also use \(\hat{P}\) for other purposes. For example, \(\hat{P}\) represents $1 of principal, and the remainder is interest. That means that your total interest payment is simply \[ \hat{I} = B(\hat{P}-1) = B\left(\frac{RT}{2} + \frac{(RT)^2}{12}\right).\]

We can also use \(\hat{P}\) to produce estimated amortization tables, which tell us how much principal remains after a given number of payments. I show how to do this later in the post.

Where Does This Approximation Come From and Why Does This Work?

The expression that most mortgage calculator websites use for your monthly payment \(M\) is the following:¹

\[M = B \left(\frac{r(1 + r)^N}{(1 + r)^{N}-1}\right) = \frac{B}{N} \left(\frac{rN}{1-(1 + r)^{-N}}\right) \] Here, \(r\) is the monthly interest rate (equal to \(R/12\)), and \(N\) is the total number of payments over the lifetime of the loan (equal to \(12 T\)). Note that \(rN = RT\); I will use these quantities interchangeably below.

The middle expression is what you will see on most websites; the second expression has been rearranged in a way that I think is more helpful for explaining what is going on. For now, I will take this expression for \(M\) as given, though eventually I hope to write a follow-up post explaining where it comes from.

The key quantity to focus on is \[P(r,N) = \frac{rN}{1-(1 + r)^{-N}}.\] This gives the exact ratio of your total payments \(MN\) to your original loan \(B\). We will apply two approximations to \(P\).

Approximation 1 \(1 - (1+r)^{-N} \approx 1 - e^{-rN}\), and thus \(P(r,N) \approx \tilde{P}(r,N)\), where \[\tilde{P}(r,N) = \frac{rN}{1-e^{-rN}}\]

This comes from the well-known approximation \(1 + r \approx e^{r}\). Conceptually, if you start a month with a $1 loan, \(1 + r\) gives your balance at the end of the month when interest is compounded monthly, and \(e^{r}\) gives your balance if interest were compounded continuously.

Interestingly, Approximation 1 actually works well for any \(r\) (not just when \(r\) is small). In particular, the relative error \(1-\tilde{P}/P\) is at most \(1/(3N)\), uniformly in \(r\). (For those interested in a deep dive into this point, see the end of the post.) This means that for a 30 year mortgage, the error in your estimated monthly payments from using \(\tilde{P}\) instead of \(P\) will be less than \(0.1\%\). Even for a \(6\) year mortgage, the error from this approximation is at most \(0.5\%\).

Important Insight. While \(\tilde{P}\) may not be much easier to calculate than \(P\), it does provide an important insight! Note that \(\tilde{P}\) is a function of the single variable \(rN = RT\). This means that if you have two loans with different \(r\) and \(N\) but the same \(rN\), the total payments over the life of the loan will be almost identical. For example, a 30-year loan at 5%, 20-year loan at 7.5%, and a 15-year loan at 10% will all lead to the same total payment. From this, it follows that the monthly payment for a 15-year loan at 10% will be double the payment for a 30-year loan at 5% (since you’re paying back the same total amount in half the time).

If \(RT \approx 1.59\), then \(\tilde{P} \approx 2\), so your monthly payment will be roughly double the interest-free rate. This occurs if, for example, you have a 20-year mortgage at an 8% interest rate.

Now it’s time to further approximate \(\tilde{P}\) to come up with the approximation \(\hat{P}\) given above.

Approximation 2 \(\frac{rN}{1 - e^{-rN}} \approx 1 + \frac{rN}{2} + \frac{(rN)^2}{12}\).

This comes from a standard Taylor expansion around \(rN = 0\). What is especially nice is that the coefficient of the cubic term of the Taylor expansion is zero, so this gives a surprisingly good approximation for most “reasonable” values of \(rN = RT\), as the following plot shows (\(\tilde{P}\) shown in bold, \(\hat{P}\) as a dashed line).

plot(function(x){return(x/(1-exp(-x)))},xlim=c(0,5),xlab='RT',ylab='Total Payments/Principal',las=1,lwd=2) #\tilde{P}
plot(function(x){return(x/(1-(1+x/360)^(-360)))},xlim=c(0,5),add=TRUE) #Exact P
plot(function(x){return(1+x/2+x^2/12)},xlim=c(0,5),add=TRUE,lty='dashed') #\hat{P}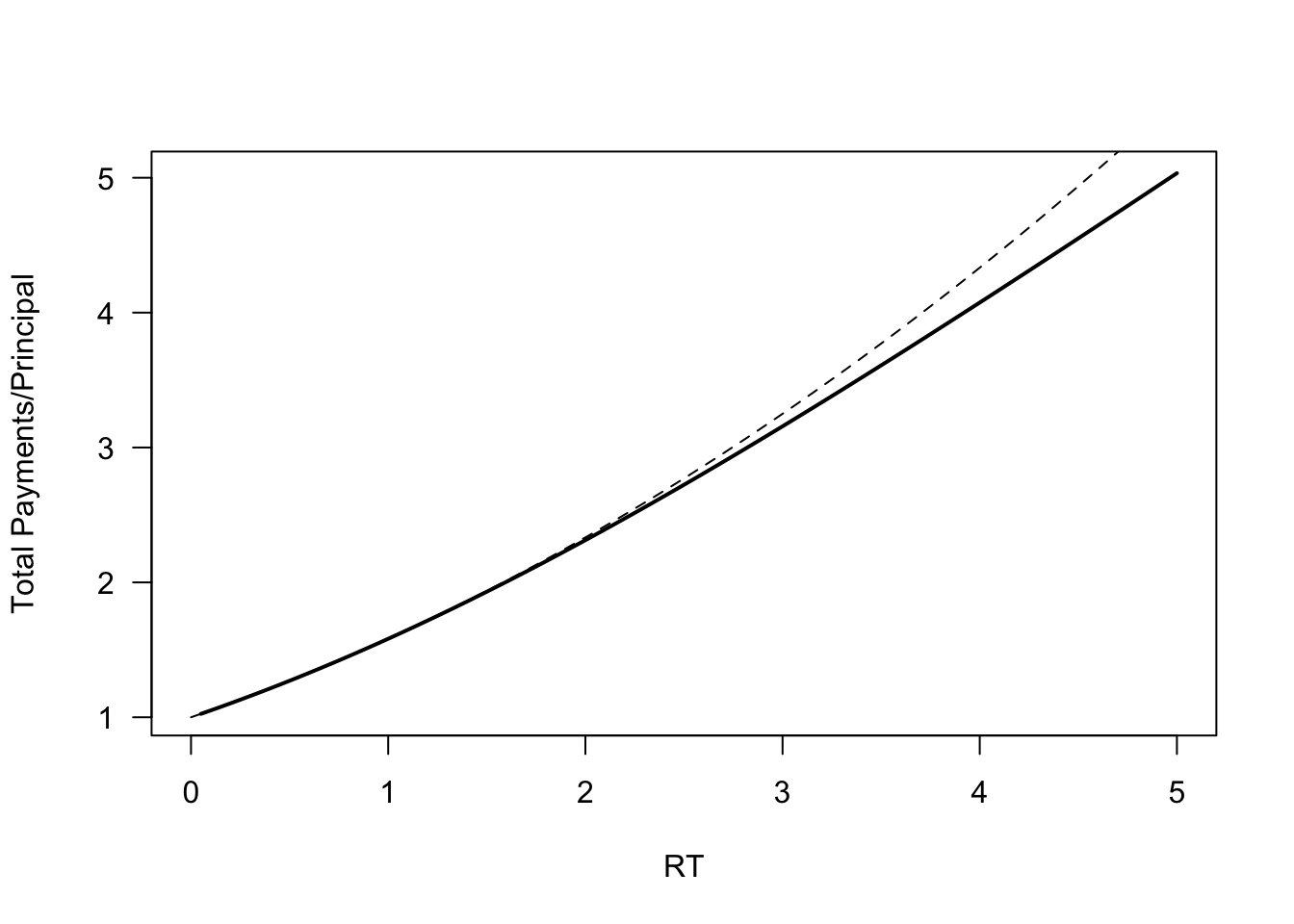

Note that our approximation \(\hat{P}\) is always an overestimate of \(\tilde{P}\). When \(RT\) is small (interest rates are low or the duration of the mortgage is short), the approximation is excellent. Our approximation is within 2% so long as \(RT \le 2.6\). For larger \(RT\), we can use a different approximation: \(RT/(1-e^{-RT}) \approx RT\). This is an underestimate of \(\tilde{P}\). If we use the estimate \[\hat{P}(r,N) = \left \{ \begin{array}{l l} 1 + \frac{rN}{2} + \frac{(rN)^2}{12} & rN < 3.3 \\ rN & rN \ge 3.3 \end{array}\right.\] then we will be within 3.7% of \(\tilde{P}\), no matter what the value of \(rN\) is, and much closer than that if \(rN\) is not too close to \(3.3\) (for most loans, \(rN < 3.3\)).

Intuition for Final Formula

I have provided an algebraic derivation for this approximation but can we find corresponding intuition?

The leading \(1\) in \(\hat{P}\) represents the principal: for every dollar you borrow, you will have to pay it back. The remaining \(\frac{rN}{2}+\frac{(rN)^2}{12}\) represents interest on that dollar.

According to this Mathematics Magazine article by Peyman Milanfar, Persians merchants used the simpler approximation that interest is principal times \(rN/2\). My “interpretation” of this term is as follows.

If you have a balance \(B\), then the amount of interest owed at the end of the month is \(Br\). If you paid this amount of interest in each of \(N\) payments, you would pay \(BrN\) in total. But over the life of the loan, your balance is changing! It starts at \(B\) and ends at \(0\), so one might expect that “on average” your balance is \(B/2\), leading to estimated interest payments of \(BrN/2\). As we will explore more completely in the next section, your average balance is in fact greater than \(B/2\), so this is an underestimate of interest paid. But it works fairly well if \(rN\) is small (within \(2\%\) if \(rN < 0.5\)). This is probably the case for many merchant loans: I doubt payments are collected over 30 years!

For values of \(rN\) that arise in home loans, the error is sizeable, so we need to include the \((RT)^2/12\) term. Interestingly, the 12 here has nothing to do with the fact that there are 12 months in a year – it just happens to be the coefficient of the corresponding Taylor expansion. I haven’t come up with a good heuristic for why this is the “right” second-order correction.

Amortization Tables

We now return to the question, “what will my principal be, as a function of the time remaining on the mortgage?” This is relevant for people who might terminate the loan early, either due to moving and selling the home, or due to refinancing.

There are many online resources explaining how to calculate your next balance, as a function of your current balance, interest rate, and monthly payment: multiply your balance by the (monthly) interest rate. This is how much of your monthly payment goes to interest; the rest goes to reducing the principal.

However, few resources explicitly give a formula for your remaining balance afer \(k\) payments. Let this be \(B_k\). We know \(B_0 = B\), and \(B_N = 0\), but what about in between? We can determine this as follows.

Recall that your monthly payment is \[M = \frac{B \times P(r,N)}{N},\] where \(P(r,N)\) has the complicated form given above, and represents the rate of dollars paid to dollars borrowed.

After \(k\) payments, I don’t know \(B_k\). But I do know that the number of remaining payments is \(N-k\), and the interest rate \(r\) has not changed. I also know that my monthly payment does not change. Therefore, I can solve \[M = \frac{B \times P(r,N)}{N} = \frac{B_k \times P(r,N-k)}{N-k}\] to get \[\frac{B_k}{B} = \left(1-\frac{k}{N}\right) \frac{P(r,N)}{P(r,N-k)}.\] The left side is the percentage of your balance that remains. \(1 - k/N\) is the percentage of the total time that remains. The factor \(P(r,N)/(P(r,N-k))\) is always bigger than \(1\) (fixing the interest rate, you pay more in total for a loan of longer duration), so this says that when \(80\%\) of the loan term remains, your principal is (sadly) more than \(80\%\) of the initial balance.

This formula is exact: it should match amortization tables that you can find online. But if we want to approximate it, we can simply plug in our estimates \(\tilde{P}\) or \(\hat{P}\) instead of the real \(P\).

If we plug in \(\tilde{P}\) for \(P\) and do some algebra, we get that your balance is approximately \[ \tilde{B}_k = B \frac{1-e^{-r(N-k)}}{1 - e^{-rN}}.\] Note that when \(k = 0\), this is the full amount, and when \(k = N\), your principal has dropped to zero.

For those of you who don’t like exponential functions, you substitute \(\hat{P}\) instead. To keep the algebra cleaner, let \(t = 1-k/N\) be the fraction of time remaining on the mortgage (so \(t = 1\) at the beginning). Then we have the approximation \[ \hat{B}(t) = B t \left(\frac{1 + \frac{rN}{2}+\frac{(rN)^2}{12}}{1 + \frac{trN}{2} + \frac{(trN)^2}{12} }\right).\] These approximations are shown in the following figure (the solid line \(\tilde{B}\), and bold dashes are \(\hat{B}\)).

R = .05
T = 30
plot(function(x){return((1-exp(-R*T*(1-x)))/(1-exp(-R*T)))},xlim=c(0,1),xlab='Fraction of Payments Completed',ylab='Fraction of Principal Remaining',las=1)
plot(function(x){return((1-x)*(1+R*T/2+(R*T)^2/12)/(1+(1-x)*(R*T)/2+(1-x)^2*(R*T)^2/12))},xlim=c(0,1),add=TRUE,lty='dashed',lwd=2)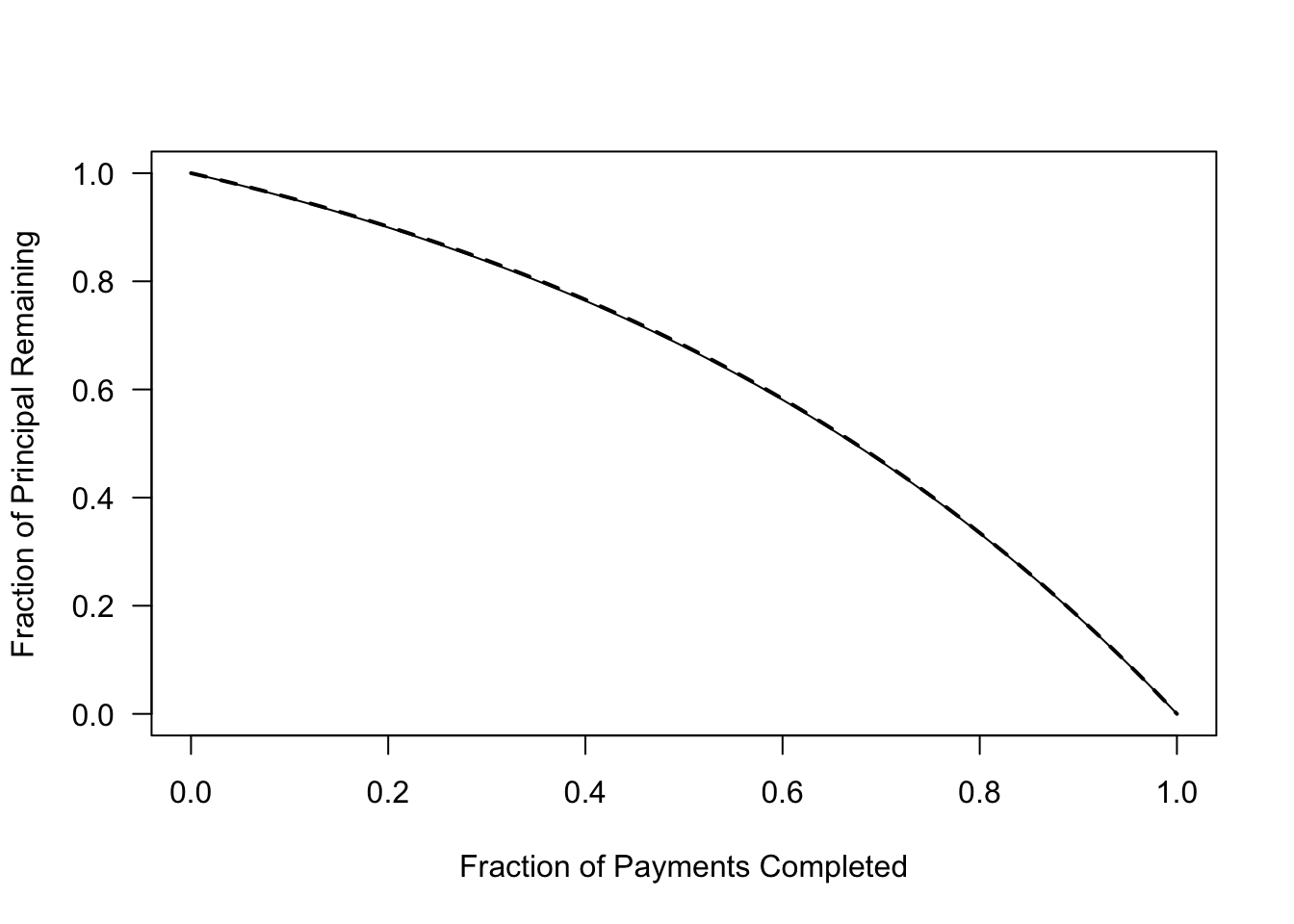

This plot shows that 2 years into a 30 year mortgage (x = 2/30), you still owe approximately 97% of the original principal. 6 years in, you are 20% of the way through, but have only paid down 10% of the balance. This illustrates that if you move houses frequently and always get a 30 year mortgage, you really won’t be building much equity (unless your home happens to appreciate significantly).

Unfinished Business: Back to Approximation 1

Why is the ratio \(\frac{1 - (1+r)^{-N}}{1-e^{-rN}}\) always so close to one? To explore this, I will do a change of variables \(x = rN\), and look at the quantity

\[1 - \frac{1 - (1+r)^{-N}}{1-e^{-rN}} = \frac{(1+r)^{-N} - e^{-rN}}{1-e^{-rN}} = \frac{(1+ x/N)^{-N} - e^{-x}}{1 - e^{-x}} = Error(x,N)\] It is easy to see that if we fix \(x\) and take \(N\) to infinity, this error vanishes. But what if we fix \(N\) and try to determine the \(x\) for which this error is largest?

It turns out that it is most helpful to plot \(N \times Error(x,N)\):

NxERROR = function(N){return(function(x){return(N*((1+x/N)^(-N)-exp(-x))/(1-exp(-x)))})}
plot(NA,xlab='rN',ylab='N x Error',las=1,xlim=c(0,5),ylim=c(0,.44))
N = c(1:4,6,12,24,48)
colors = rainbow(length(N))
for(i in 1:length(N)){
  plot(NxERROR(N[i]),add=TRUE,col=colors[i],xlim=c(0,5))
}
legend(4.3,.45,legend=N,col=colors,lwd=2)

There are two things to notice. First, as \(N\) grows, the global maximum \(\max \limits_{x}N \times Error(x,N)\) increases. Second, the function \(N \times Error(x,N)\) actually converges pointwise as \(N \rightarrow \infty\) to the function \(e(x) = \frac{x^2 e^{-x}}{2(1-e^{-x})}\). Wolfram Alpha gives an exact maximizer of \(e\) that uses the “product log” function, but numerically, this function attains a maximum value of \(0.324\) at \(x \approx 1.59\). This implies that the relative error of replacing \(P\) with \(\tilde{P}\) is at most \(0.33/N\). Since \(N\) is the total number of payments, the error is already quite good (within 1%) even for a 3 year mortgage.

Interestingly, the value of \(x = rN\) that maximizes the error is exactly the value at which your estimated interest payments are equal to the principal (i.e. the amount you pay back is exactly double the amount you borrowed). I don’t have a good explanation for why this should be the case, but if you do, I’d love to hear it!