A Visual Approach
Suppose that we produce q copies. For each n \in \{1, \ldots, q\}, the probability that we sell our (n+1)^{st} copy is 1 - F(n). By linearity of expectation, our total expected sales can be calculated by adding up the sales probabilities of individual items: S(q) = \mathbb{E}[\min(D,q)] = \sum_{n = 0}^{q-1} (1 - F(n)).
Let’s “see” this visually. Start by plotting the cdf F. Then draw a vertical line at the proposed production quantity q. The equation above implies that our total expected sales S(q) is the area of the region to the left of our order quantity and above F. In Figure 1, this region is shaded in blue. Once we know our expected sales, we can calculate two other quantities of interest. First, expected excess inventory is q - S(q), which is equal to the area of the red region. Second, expected lost sales (from lack of inventory) is equal to \mathbb{E}[D] - S(q), which is equal to the area of the orange region.
Now, we can see the consequences of changing our production quantity: as we move the vertical line to the right, sales increase (lost sales decrease), but so does expected excess inventory! We want to choose our order quantity to strike an appropriate balance: that is, to minimize a weighted sum of the red and orange regions.
This is where the economics of the situation come in. The red and orange regions represent excess inventory and lost sales in quantities of games. We want to translate these to dollars. The critical ratio tells us how costly “overage” is relative to “underage.” More specifically, it tells us how often we should have excess inventory when ordering optimally. We can plot the critical ratio as a horizontal line. This line intersects the demand distribution F at the optimal order quantity.
plotnews = function(cr,F,qMin = 0, qMax,q){
plot(F,xlim = c(qMin,qMax), ylim=c(0,1),ylab='P(Excess Inventory)',yaxs='i',xaxs='i',xlab='Order Quantity',las=1) #Plot Demand Distribution
x = c(qMin:qMax)
y = F(x)
polygon(c(x[1:q],x[q],0),c(y[1:q],1,1),col='light blue') #Expected Sales
polygon(c(x[1:q],x[q],0),c(y[1:q],0,0),col='red') #Expected Excess Inventory
polygon(c(x[q:qMax],x[q],x[q]),c(y[q:qMax],1,1),col='orange') #Expected Lost Sales
abline(h=cr) #Plot Critical Ratio
}
cr = 0.6
mean = 100
sd = 30
qStar = ceiling(qnorm(cr,mean,sd))
qMax = mean+3*sd
F = function(x){return(pnorm(x,mean,sd))}
plotnews(cr,F,qMin = 0,qMax,qStar)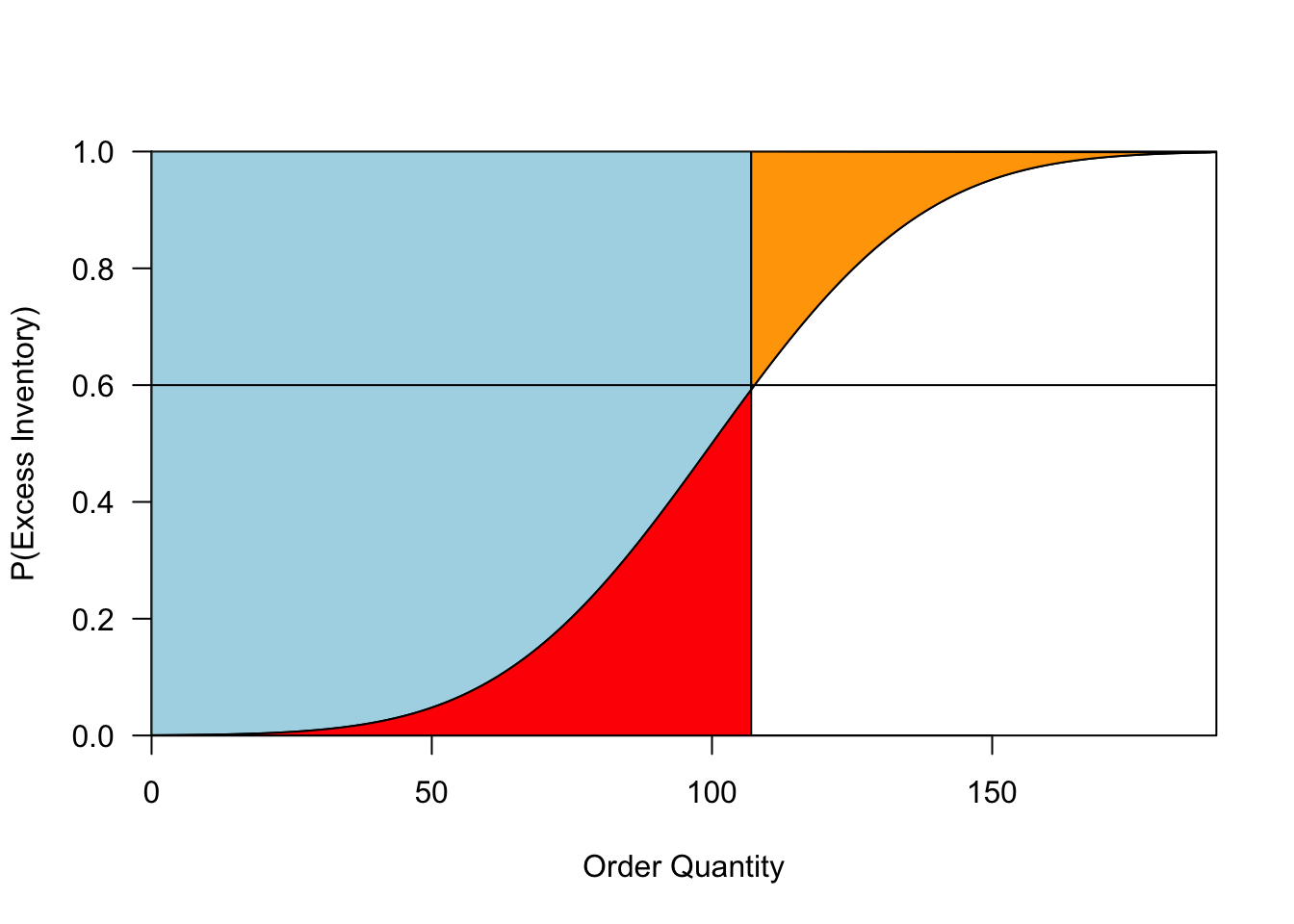
Figure 1: A visualization of the classical newsvendor problem. The curve represents the CDF of the demand distribution. The vertical line gives our order quantity. The blue region represents expected sales, and the red and orange regions represent expected overage and underage, respectively. The horizontal line shows our critical ratio: the optimal order quantity is where this line intersects the demand distribution.
To me, the resulting picture is beautiful. It captures so much about the problem! We know that we’re trying to adjust the production quantity (vertical line) to balance overage (red) and underage (yellow). To determine an optimal order quantity, we need both a demand forecast (F) and an understanding of the relative costs of overage and underage (the critical ratio). Each of these is represented by a single curve in Figure 1.
Several insights arise.
No matter what demand distribution you draw, you should order so that our probability of excess inventory is equal to the critical ratio.
As the critical ratio increases, so does our optimal production quantity, as shown in Figure 2. When you have a lot of certainty about demand, the distribution F will rise very steeply. In these cases, changes to the critical ratio do not have a large effect on our production quantity: you roughly produce to match demand. Meanwhile, when demand is very uncertain, the distribution F will be flatter, and the critical ratio will greatly influence our order.
As you become more certain about demand, F becomes steeper and both the red and orange regions shrink, as shown in Figure 3. Thus, increased certainty does not change our chance of having overage or underage (see the first insight), but it does decrease the expected amount by which you err. Note also that increased certainty could either increase or decrease your optimal order. Your order will decrease when your critical ratio is high and you were previously hedging by over-ordering (as shown in 3); it will increase when your critical ratio is low.
You don’t need perfect demand information to make reasonable ordering decisions. For example, you can assess whether our current policy systematically over-produces or under-produces using only the critical ratio and knowledge of how frequently you sell out. In addition, if our critical ratio is bounded away from 0 or 1, then you don’t need to account for very rare events that dramatically shift demand.4
plotnews(cr,F,qMin = 0,qMax,qStar)
crNew = 0.8
qNew = ceiling(qnorm(crNew,mean,sd))
abline(h=crNew)
arrows(qStar-1,cr,qStar-1,crNew,lwd=2) #Increase in CR
arrows(qStar-1,crNew,qNew,crNew,lwd=2)
text(85,(cr+2*crNew)/3,"Increased")
text(85,(2*cr+crNew)/3,"Critical Ratio")
text(122,0.93,"Increased")
text(122,.87,"Order")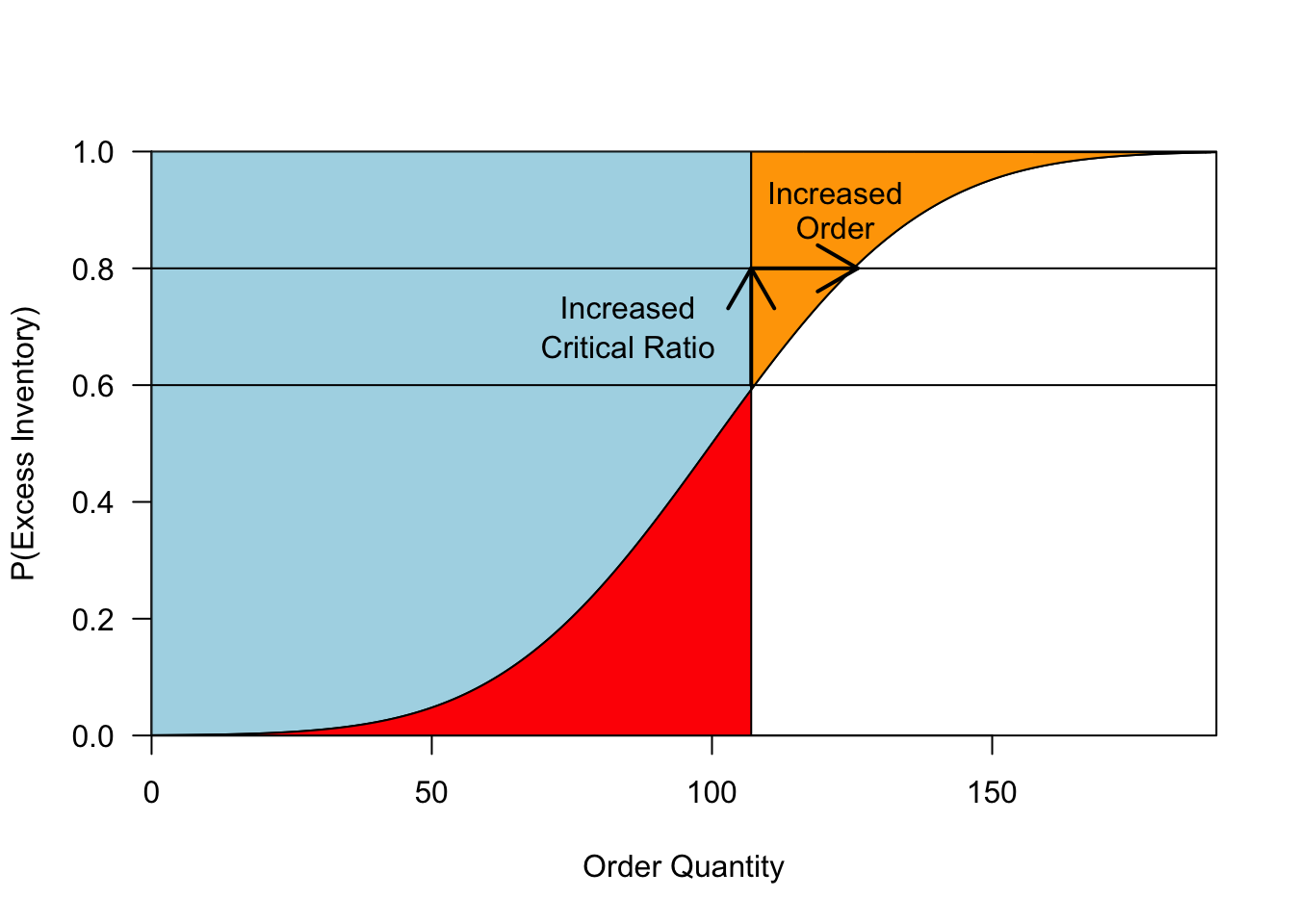
Figure 2: As the critical ratio increases, so does the optimal order quantity. The rate of increase is largest when demand is very uncertain.
cr = 0.8
plotnews(cr,F,qMin=0,qMax, q = ceiling(qnorm(cr,mean,sd)))
sd = 15
plotnews(cr,F,qMin=0,qMax, q = ceiling(qnorm(cr,mean,sd)))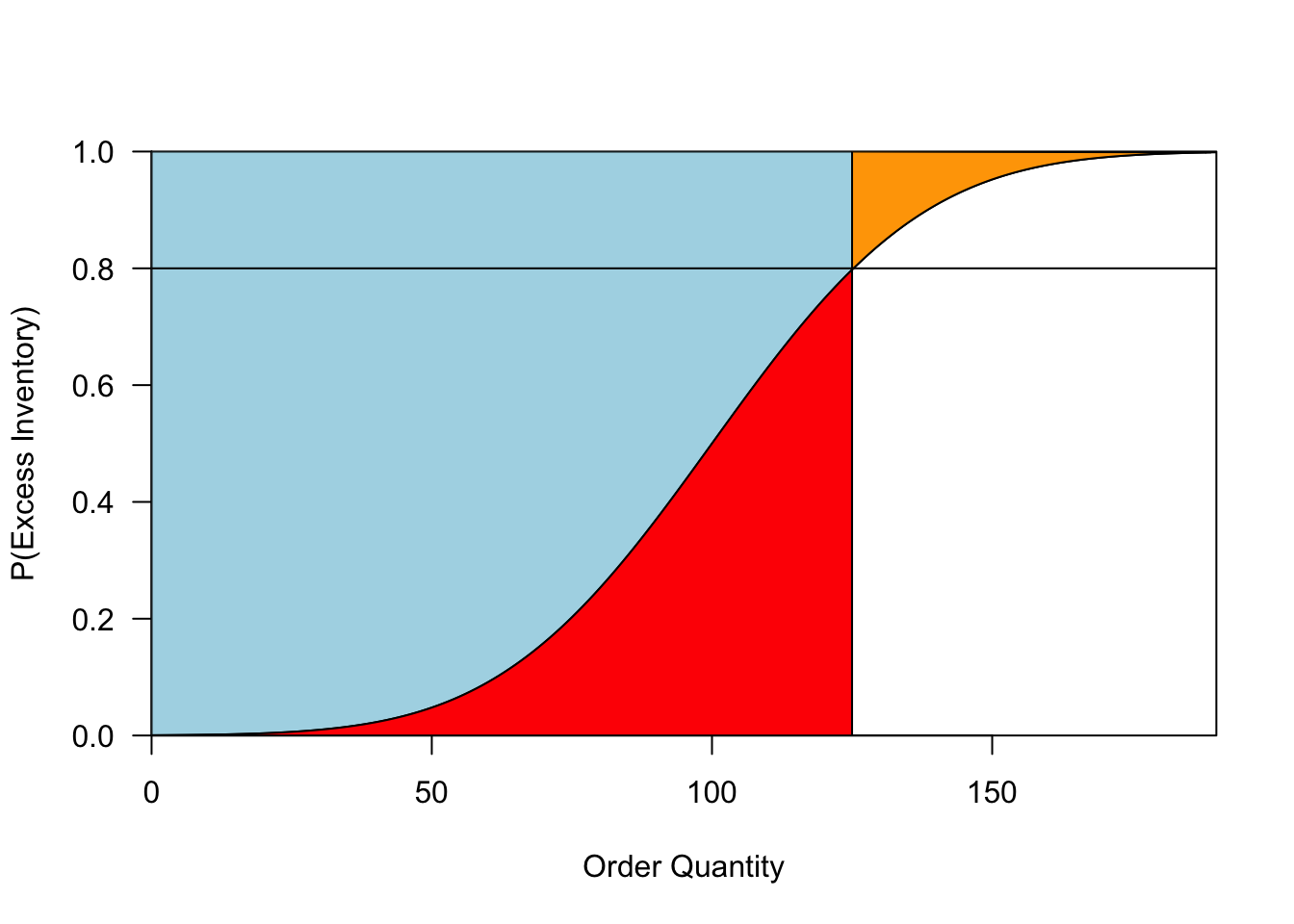
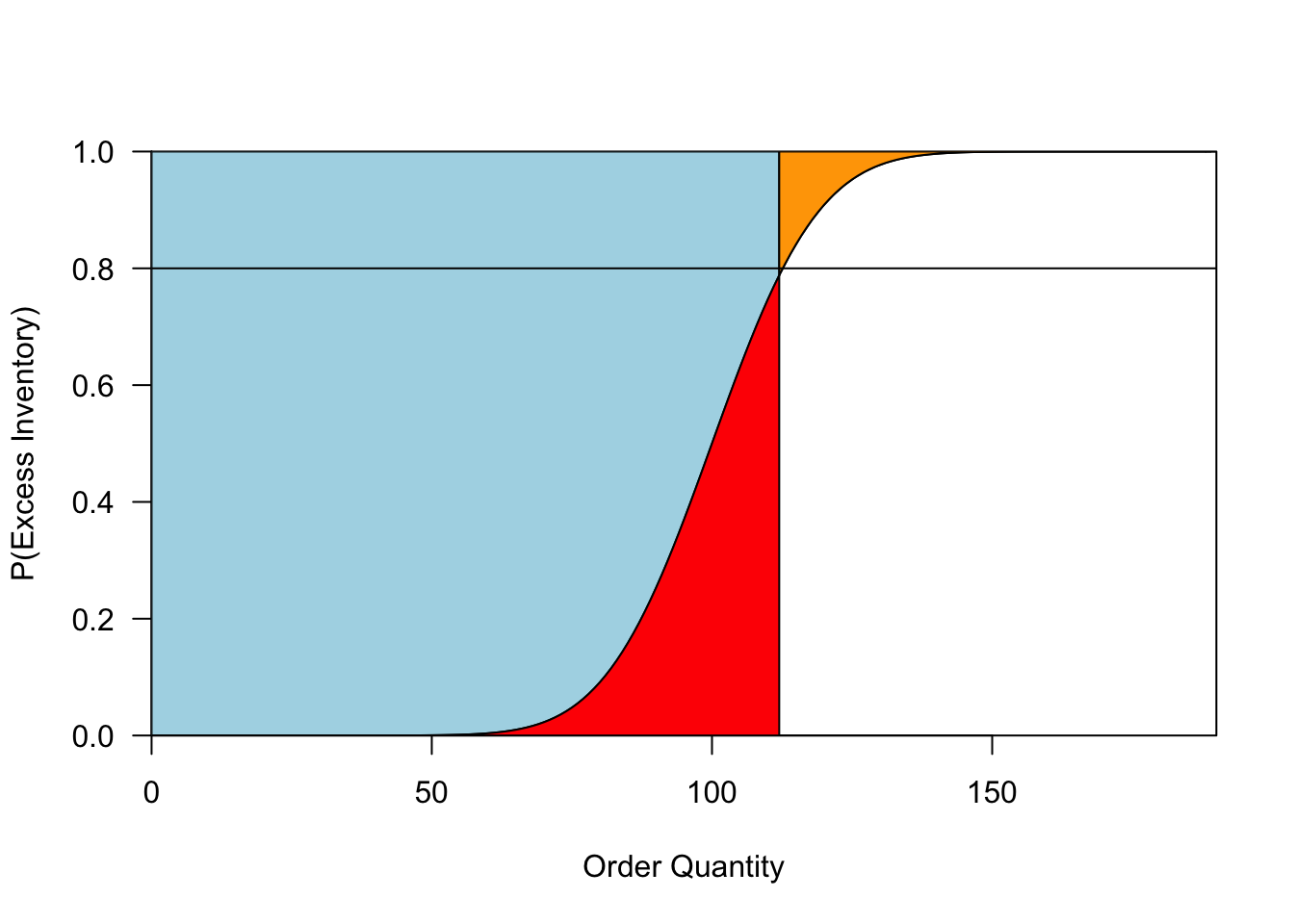
Figure 3: Outcomes when demand is uncertain (left) and more certain (right). When ordering optimally, the probability of having some overage is the same in both cases, but the expected overage and underage (in red and orange, respectively) is much lower when demand is more certain.