Analysis
We now turn to the two questions above. First, what is the value of offensive rebounding?
You might measure this by looking at the increase in points per possession as a result of an increase in offensive rebounding rate.1 However, this doesn’t directly address the relative value of shot-making and offensive rebounds.
To do this, we can compare two teams, one of which (team ‘Dan’) has a higher shooting percentage than the other (team ‘Nick’). We can ask, ‘How much higher does team Nick’s offensive rebounding have to be, in order to have the same points per possession?’ Let’s start assuming NBA scoring. Suppose that Dan makes 1/3 of his shots, but never graps an offensive rebound.2 Thus, on average he scores 1/3 of a point per possession. Nick makes only 20% of his shots. What must his offensive rebounding rate be to match Dan’s 1/3 points per possession? The answer is 50%.
We can carry out this exercise for varying and . Figure 1 displays curves of equivalent teams. The red curve corresponds to teams that score of a basket per possession, and includes both team Dan at (1/3,0) and team Nick at (1/5,1/2).
alphaNBA = function(p,v){return(1-p/(1-p)*(1/v-1))}
V = c(1:5)/6
plot(NULL,xlim=c(0,1),ylim=c(0,1), xlab='Shooting Percentage',ylab='Offensive Rebounding Rate',las=1,xaxs='i',yaxs='i',xaxt='n')
axis(1,at=c(0:6)/6,labels=c('0','1/6','2/6','3/6','4/6','5/6','1'))
for(v in V){ plot(Vectorize(function(p){return(alphaNBA(p,v))}),add=TRUE) }
plot(Vectorize(function(p){return(alphaNBA(p,1/3))}),col='red',add=TRUE)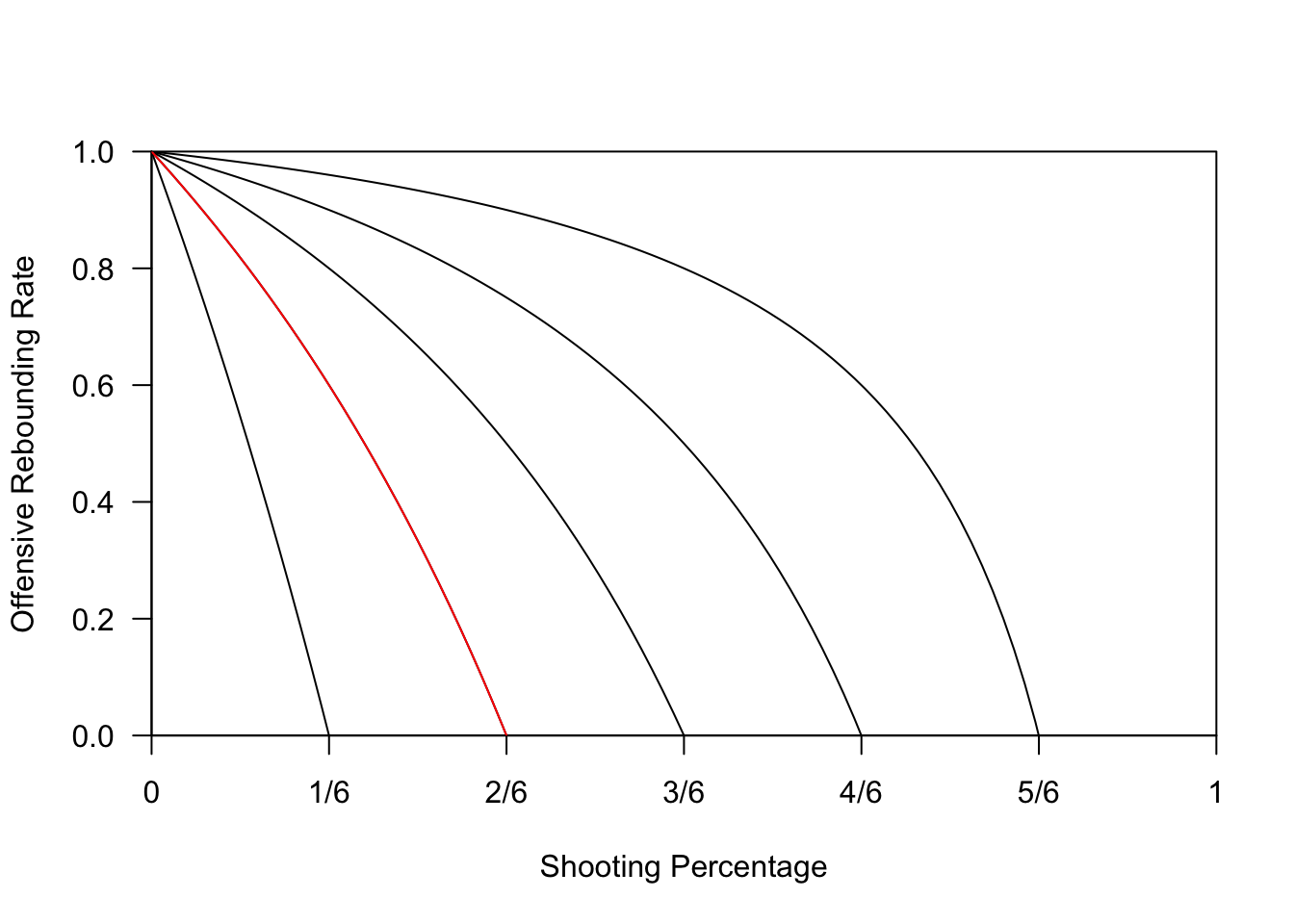
Figure 1: Each curve identifies teams with the same points per possession (x-intercept).
Overall, my reaction is that these curves are disappointingly steep. That is, it takes a large increase in offensive rebounding proficiency to offset a small decline in shooting percentage.3 Perhaps under pickup rules, the value of rebounding is higher? After all, if you grab a rebound, you are potentially giving your team a series of baskets, instead of one.
We can tackle this question by asking which team above (Dan or Nick) scores more points per possession under pickup rules. Recal that they were equal under NBA rules, at 1/3 of a point per possession. If team Nick scores more than team Dan under pickup rules, we can conclude that offensive rebounding is more valuable under pickup rules.
Crunching the numbers, we see that under pickup rules, both teams expect to score 0.5 points per possession! I initially found this surprising – did I just happen to choose special numbers? Turns out, the answer is ‘no.’ We can see this by inverting our expressions above to get “possessions per point.” We see that this is under NBA rules, and under pickup rules. This immediately implies the following result, which I interpret to mean that the rule set (pickup vs NBA) doesn’t really affect the relative value of the two skills.
Proposition. Consider team , with shooting percentage and offensive rebounding rate , and team with shooting percentage and offensive rebounding rate . If scores more points per possession than under pickup rules, then the same is true under NBA rules (and vice versa).
Of course, shooting is a skill that doesn’t necessarily translate to defense, whereas good offensive rebounders are presumably also good defensive rebounders. The reasoning above could also be used to quantify the value of good on-ball defense (lowering the opponent’s ) and good defensive rebounding (lowering their ). However, at this point I think my time would be better spent working on my shot at the gym, rather than working through math trying to justify my value to the team.