Rationing Medical Supplies | b

Rationing Medical Supplies

Nick Arnosti

2020/06/05

 

Overview

The Coronavirus pandemic has resulted in a need to ration scarce medical supplies. Most people agree that test kits, ventilators, antiviral medication, and vaccines should not necessarily go to those willing to pay the most for them. States have been revising their allocation guidelines to reflect various ethical considerations.1

One question that emerges is whether to give priority to certain categories of people, such as emergency personnel. A recent working paper by Parag Pathak, Tayfun Sonmez, Utku Unver, Bumin Yenmez examines existing guidelines, and notes that some states prioritize emergency personnel, whereas others (including my home states of New York and Minnesota) do not.2 Their conclusion is that most people wish to give some advantage to emergency personnel, but are afraid that doing so might result in all units going to these personnel, at the exclusion of other groups.

My interpretation of this conclusion is the following. Suppose we look at the success rate of emergency personnel (among emergency personnel who needed the resource, how many got it?), and the success rate of the rest of the population. Call the ratio of these success rates the advantage granted to emergency personnel. That is, if 10% of emergency personnel get the resource, and only 2% of people who are not emergency personnel do, then emergency personnel have an advantage of 5. It seems (and I would welcome comments on this assertion, as I am not an ethicist) that most people would like emergency personnel to have some advantage \(> 1\), but for this advantage to not be too large.

How can we ensure this? The aforementioned paper proposes a system that reserves certain units for emergency personnel, while making other units available to anybody.3 In this post, I observe that under a reserve policy, it is hard to control or predict the advantage offered to medical personnel.4 I then consider an alternative: policymakers could directly specify their desired advantage.

A Simple Model

There is a finite set of privileged categories \(C\), and a ranked list of \(n\) applicants. (I will be agnostic about where this ranking comes from: an applicant’s position could be determined by their medical condition, by lottery, or other considerations.) Each applicant to at most one category. Let \(C_0\) denote the set of categories, along with the empty set (indicating someone who does not belong to any of the categories in \(C\)). A priority list of length \(n\) is simply an element \(L \in C_0^n\). For each \(c \in C_0\), let \(n_c\) denote the number of applicants belonging to category \(c\).

There are \(m\) identical units to be allocated. An allocation function takes as input the priority list \(L\) and produces as output the number \(m_c\) of units allocated to each category \(c\). Within each category, units are always awarded to the highest-priority applicants. The success rate of category \(c\) is the fraction of applicants who receive units, given by \(s_c = m_c/n_c\). The advantage of category \(c\) is the ratio \(s_c/s_0\).

To keep things simple, much of the post will assume that there is only one privileged category (emergency personnel).

Reserve Policies

Suppose that there are \(m = 20\) units, and we decide to reserve \(r = 6\) of them for emergency personnel. There are many ways to implement this reserve. We will focus on two approaches described by Pathak, Sonmez, Unver, and Yenmez:5

If the priority list is determined by lottery, these implementations correspond to policies discussed in my blog post on H1B visa lotteries: Minimum Guarantee corresponds to what I called “Single Lottery,” and Over and Above corresponds to “General Lottery First.” The following result is easily seen.

Proposition 1 For any fixed reserve \(r\), the “Over and Above” policy gives at least as many units to emergency personnel as the “Minimum Guarantee” policy. Under both policies, the number of units assigned to emergency personnel is weakly increasing in the reserve \(r\).

The monotonicity condition implies that in some sense, the effect of imposing a reserve is straightforward: it benefits emergency personnel, with greater benefit the larger the reserve. However, the magnitude of this benefit is not clear at the time the reserve is set.

We can see this uncertainty in the following figure, which shows that the advantage implied by a given reserve can vary greatly depending on the proportion of emergency personnel in the applicant pool.

#Based on fluid model with priorities determined by lottery.
#Normalize mass of agents to one
#Parameters are q (mass of units), p (percentage of population that are doctors)
#Mechanisms given by r (reserve percentage) and alpha (advantage) > 1

quantity_to_doctors_minimum_guarantee = Vectorize(function(p,q,r){
    return(min(p,q*max(p,r)))
})

quantity_to_doctors_over_above = Vectorize(function(p,q,r){
    return(min(p*q*(1-r)+r*q,p))
})

quantity_to_doctors_advantage = function(p,q,alpha){
    regular_win_prob = uniroot(function(x){return((1-p)*min(x,1)+p*min(alpha*x,1) - q)},interval=c(0,1))$root 
    return(p*min(regular_win_prob*alpha,1))
}

advantage = Vectorize(function(p,q,quantity_to_doctors){
    return(quantity_to_doctors/p*(1-p)/(q-quantity_to_doctors))
})



#Plotting advantage under each reserve system, as function of p
q = .2
r = .5
par(mar = c(5,5,1,2))
plot(Vectorize(function(p){return(advantage(p,q,quantity_to_doctors_minimum_guarantee(p,q,r)))}),las=1,xlab='Fraction Who Are Emergency Personnel',ylab='Advantage',ylim=c(0,10),cex.lab=2,cex.axis=2)
plot(Vectorize(function(p){return(advantage(p,q,quantity_to_doctors_over_above(p,q,r)))}),lty='dashed',add=TRUE)
legend(.3,9,legend = c("Minimum Guarantee","Over and Above"), lty=c('solid','dashed'),cex=1.5)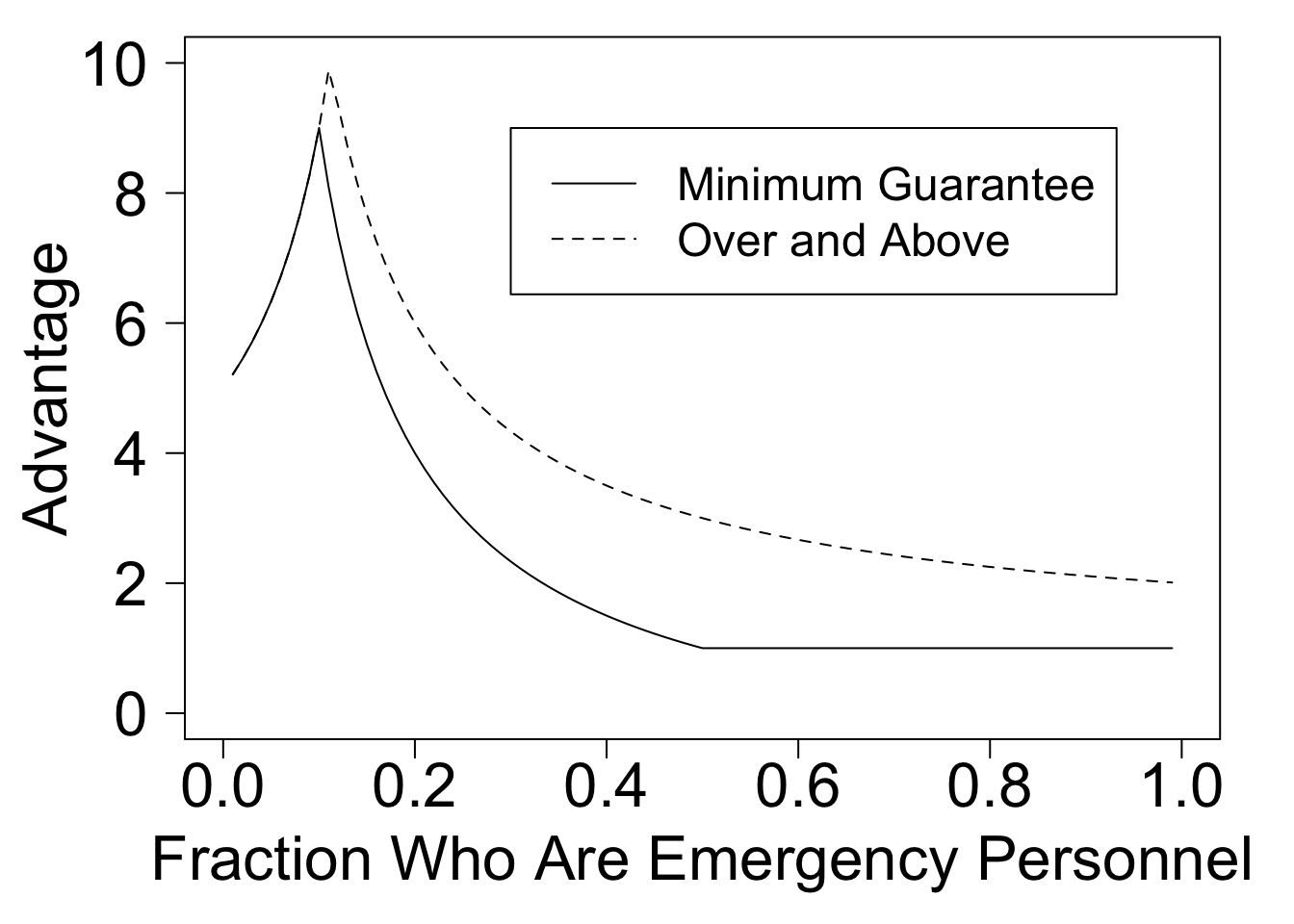
Reserving 50% of units for emergency personnel results in an unpredictable advantage.

Figure 1: Reserving 50% of units for emergency personnel results in an unpredictable advantage.

The “Specified Advantage” Policy

Here’s a mechanism that addresses this concern. It is parameterized by desired advantages \(\alpha_c \geq 1\) for each category \(c \in C_0\) with \(\alpha_0 = 1\). Solve for the success rate \(s_0\) using the following equation:

\[ \sum_{c \in C_0} n_c \min(s_0 \alpha_c,1) = m. \] Then allocate \(m_c = n_c \min(s_0 \alpha_c,1)\) units to applicants from category \(c\) (for simplicity, I am ignoring rounding errors). The quantity \(s_0\) gives the success rate among the general population. For categories with \(\alpha_c > 1/s\), all applicants from that category receive a unit. For all other categories, the success rate is exactly \(\alpha_c\) times \(s_0\).

If the composition of the list is known in advance, then one can get exactly the same outcomes using this policy as using a reserve policy.

Proposition 2 (Equivalence) Fix the priority list \(L\) and the number of units \(m\). Let \(|C| = 1\). For any reserve \(r < m\),

However, if the composition of the priority list is unknown, this mechanism ensures a specified advantage for emergency personnel.

Closing Thoughts

This post considers two ways to advantage a target group such as emergency personnel.

I can imagine scenarios where either form of guarantee is more desirable than the other. To me, comparing success rates seems natural. If priorities are determined by lottery, the specified advantage mechanism is a form of weighted lottery in which policymakers directly specify lottery weights. If the priority list is not generated by lottery, the specified advantage policy has several potentially undesirable features, and I would hesitate to use it.7 However, I am not concinced that a reserve system – which offers a large advantage if the priority list contains few essential personnel, and little to no advantage if it contains many essential personnel – will be easy for policymakers to use appropriately.

I’d love to hear from you about i) whether the concept of “advantage” defined here seems like a reasonable measure, and ii) alternative allocations procedures that you think should be considered!

  1. My friend Brendan Parent has helped to craft the guidelines for New York State.↩

  2. This Freakonomics Podcast provides an accessible discussion of their work and other ideas related to medical rationing.↩

  3. Excitingly, they are also collaborating with the University of Pittsburgh to bring these ideas to practice. Reserve systems are already used in many contexts, including the allocation of public school seats, H1B Visas, and government jobs in India.↩

  4. Perhaps for this reason, reserve policies have often produced surprising and unintended consequences. For example, in Boston, a system that reserved half of the seats at each school for neighborhood children was found to be nearly equivalent to a system that gave no advantage to these children. In India, affirmative action policies have been implemented in a manner that sometimes hurts the intended beneficiaries!↩

  5. Both of these approaches use a “soft” reserve, meaning that if there are fewer than six emergency personnel, excess reserved units are given to members of the general public. Furthermore, under both approaches, emergency personnel remain eligible for unit that are available to the general public, ensuring that an applicant is never hurt by their emergency status.↩

  6. The Over and Above policy can also have no effect, although this is much less likely: in our example, there is no benefit only if emergency personnel occupy positions 15-20 on the priority list.↩

  7. For example, an individual might be harmed by revealing that they are medical personnel. In addition, it fails to satisfy an “irrelevance of rejected applicants” condition: the presence of low-priority emergency personnel (who will never win a unit) can shift units from the general population to other emergency personnel.↩