I found this puzzle on Twitter, suggested by Max Resnick:
You are given a 6 sided die. You may roll it as many times as you want. After any roll you can choose to stop and receive a payoff equal to the average of all your die rolls up to that point. What is the optimal stopping rule?
I fed this prompt into ChatGPT o1. It produced a bunch of “analysis” which I will spare you, followed by this conclusion:
From the above analysis, the optimal policy is:
Continue rolling as long as your current average \(\bar{X}_n\) is below 3.5. Stop as soon as your average \(\bar{X}_n\) is at least 3.5. Under this policy, your final expected payoff turns out to be 3.5.
The last sentence is clearly wrong. If I only stop when my value is at least 3.5, then clearly, my average ending value is above 3.5! Furthermore, stopping as soon as my value reaches 3.5 is not optimal: while I should certainly never stop if my value is below 3.5 (I can always get to 3.5 by just continuing to roll), I sometimes want to continue even if my value is above 3.5 (as we will explore later).
One of the responses to Max’s post suggested being greedier:
With infinite rolls you will very likely have an average > 5 at some point. Don’t know when to stop but wouldn’t take less than 5 as a heuristic.
I see the appeal to this: If I only stop when the average value is above \(5\), then surely my reward will be above \(5\)! Unfortunately, the conclusion “you will very likely have an average > 5 at some point” is not correct: the average will settle down close to 3.5, and has a positive probability of never reaching 5. We can (sort of) see this in the following plot.
set.seed(281224)
max_rolls = 50
n_trials = 4
rolls = matrix(sample(1:6,n_trials*max_rolls,replace=TRUE),nrow=max_rolls)
averages = apply(rolls,2,cumsum)/(1:max_rolls)
plot(NA,xlim=c(1,max_rolls),ylim=c(1,6),xlab='Number of Rolls',ylab='Sample Avg',las=1)
for(i in 1:n_trials){lines(averages[,i],col=rainbow(n_trials)[i],lwd=2) }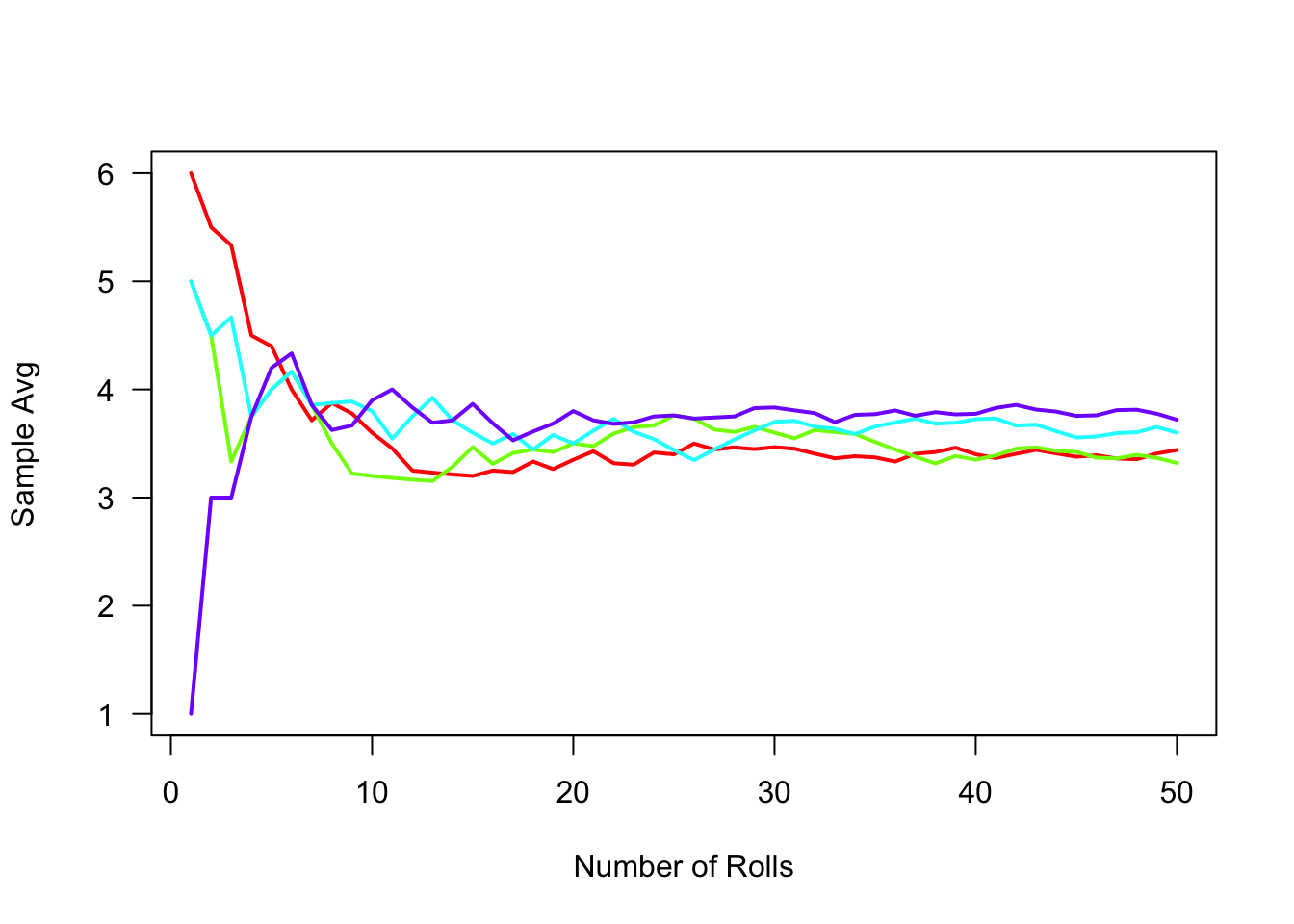
This plots the result of four trials (each capped at 50 rolls to make the plot readable). In each case, the sample average reaches its maximum fairly early on before settling down.
Comparing “Stop over 3.5” to Omniscient
What we can easily do is run a lot of trials, and compare the reward of the strategy suggested by GPT (which again, is not optimal) to the strategy of an “omniscient” player who can see the future (alternatively, someone who can roll forever and then go back and choose when to stop).
max_rolls = 500
n_trials = 100000
rolls = matrix(sample(1:6,n_trials*max_rolls,replace=TRUE),nrow=max_rolls)
averages = apply(rolls,2,cumsum)/(1:max_rolls)
max_avg = apply(averages,2,max)
stop_gpt = apply(averages,2,function(seq){if(all(seq<=3.5)) return(seq[length(seq)]); return(seq[which(seq>3.5)][1])})
mean(stop_gpt) #Reward from GPT strategy ## [1] 4.370825mean(apply(averages,2,max)) #Reward to omniscient player## [1] 4.563184This shows that the “stop over 3.5” strategy gets an average reward of approximately 4.37, while the omniscient player gets an average reward of approximately 4.56.
Solving for the Optimal Strategy
What about the optimal strategy? We can tackle this using dynamic programming. We will modify the game to assume that you must stop after at most \(N_{MAX}\) rolls. When \(N_{MAX}\) is sufficiently large, this additional constraint will have little effect on the game’s value.
Let \(V(S,n)\) be the value, under optimal play, of having rolled a total sum of \(S\) after \(n\) rolls. Then if \(n = N_{MAX}\), \(V(S,n) = S/n\). Otherwise, we have the recursion \[V(S,n) = \max(\frac{S}{n}, \frac{1}{6}\sum_{r=1}^6 V(S+r,n+1)).\]
I asked GPT o1 to write code to solve this value function, and it produced the following memoized function in python.
from functools import lru_cache
import matplotlib.pyplot as plt
from functools import lru_cache
import matplotlib.pyplot as plt
# ---------------------------
# 1. Parameters
# ---------------------------
N_MAX = 400 # artificial cap on the number of rolls
# ---------------------------
# 2. Value function with memoization
# ---------------------------
@lru_cache(None)
def V(S, n):
"""
Maximum expected value if you have:
- Sum of rolls = S
- Number of rolls so far = n
and you now choose optimally between stopping vs. rolling again.
"""
# If we've reached or exceeded our artificial max, must stop
if n >= N_MAX:
return S / n if n > 0 else 0.0
# If n == 0, there's no average yet; define "stop payoff" suitably
stop_value = 0.0 if n == 0 else (S / n)
# Compute the expected value if we roll again
roll_value = 0.0
for x in range(1, 7):
roll_value += V(S + x, n + 1)
roll_value /= 6.0
return max(stop_value, roll_value)
def recommend_action(S, n):
"""
Decide 'stop' or 'roll' at state (S, n),
by comparing stop_value to the expected roll_value.
"""
# If no rolls so far, typically you'd roll
if n == 0:
return "roll"
stop_value = S / n
roll_value = sum(V(S + x, n + 1) for x in range(1,7)) / 6.0
return "stop" if stop_value >= roll_value else "roll"
def main():
# First, let's just compute the "game value" if you start from scratch
# by rolling once. (You could also define V(0,0) in some manner.)
ev_start = sum(V(x, 1) for x in range(1, 7)) / 6.0
print(f"Estimated game value if starting fresh (roll #1) = {ev_start:.4f}")
# Prepare lists to store (n, average) for plotting
n_list = []
avg_list = []
# ---------------------------
# Find the smallest S that triggers 'stop' for each n
# ---------------------------
for n in range(1, N_MAX):
min_S_for_stop = None
# Minimum sum for n rolls is n, maximum is 6n
for S_val in range(n, 6*n + 1):
if recommend_action(S_val, n) == "stop":
min_S_for_stop = S_val
break
if min_S_for_stop is not None:
avg = min_S_for_stop / n
n_list.append(n)
avg_list.append(avg)
if n < 11:
print(f"n={n:2d}: smallest S that triggers 'stop' is {min_S_for_stop} (avg={avg:.3f})")
# ---------------------------
# Plot the results
# ---------------------------
plt.figure(figsize=(8, 6))
plt.plot(n_list, avg_list, 'o-', label="Smallest Average Triggering Stop")
plt.xlabel("n (number of rolls)")
plt.ylabel("S / n (smallest average that triggers stop)")
plt.title("Threshold Averages Triggering 'Stop' by Number of Rolls")
plt.grid(True)
plt.legend()
plt.show()
if __name__ == "__main__":
main()## Estimated game value if starting fresh (roll #1) = 4.4366
## n= 1: smallest S that triggers 'stop' is 5 (avg=5.000)
## n= 2: smallest S that triggers 'stop' is 9 (avg=4.500)
## n= 3: smallest S that triggers 'stop' is 13 (avg=4.333)
## n= 4: smallest S that triggers 'stop' is 16 (avg=4.000)
## n= 5: smallest S that triggers 'stop' is 20 (avg=4.000)
## n= 6: smallest S that triggers 'stop' is 24 (avg=4.000)
## n= 7: smallest S that triggers 'stop' is 28 (avg=4.000)
## n= 8: smallest S that triggers 'stop' is 32 (avg=4.000)
## n= 9: smallest S that triggers 'stop' is 35 (avg=3.889)
## n=10: smallest S that triggers 'stop' is 39 (avg=3.900)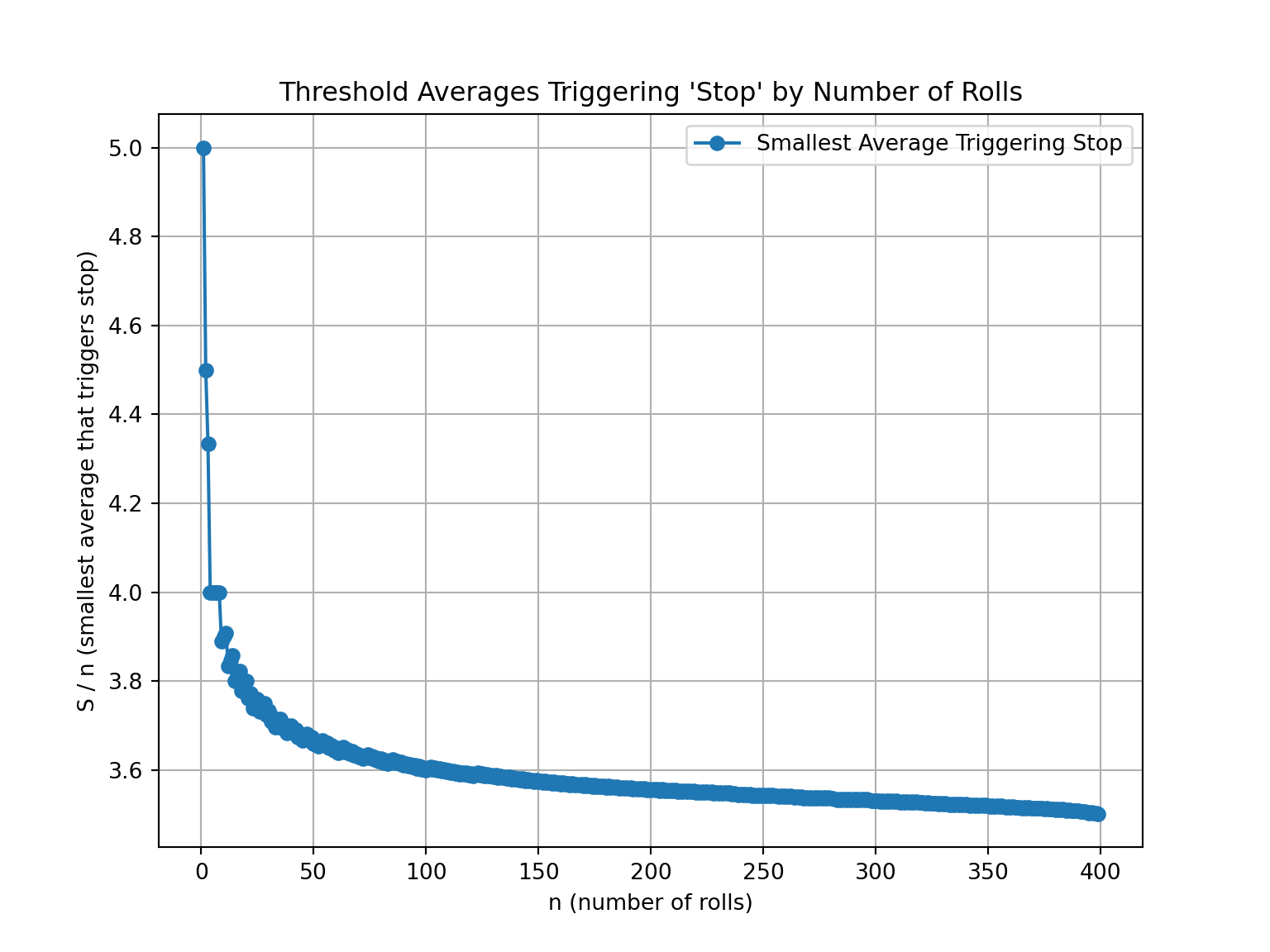 This says that (i) the estimated value of the game is approximately \(4.44\), and (ii) the lowest average required for “stop” to be the right decision decreases from 5 on the first roll, to \(4.5\) on the second, to \(3.9\) on the tenth, to 3.5 as the number of rolls approaches \(N_{MAX}\).
This says that (i) the estimated value of the game is approximately \(4.44\), and (ii) the lowest average required for “stop” to be the right decision decreases from 5 on the first roll, to \(4.5\) on the second, to \(3.9\) on the tenth, to 3.5 as the number of rolls approaches \(N_{MAX}\).
Take Home Messages
- Although tools like ChatGPT o1 are amazing in many ways, they still produce very wrong answers on simple logic and probability puzzles.
- These tools are quite useful for writing code (above, the code appears to be correct, even though the logical conclusions reached by GPT were not).
- Dynamic programming is cool.
- Although the “stop over 3.5” strategy is not optimal, it is not too far off (average reward of 4.37 instead of 4.44 for optimal).
- Even an omniscient player who sees the future can only get approximately 4.56