Note: this post is closely related to my video The Virtues of Random Priority and blog post Famous Open Question Resolved… since 2014?!?!, although it is written to be self-contained.
Motivation
When giving away resources, two natural goals are to allocate these resources efficiently and fairly. Achieving these goals requires asking people about their preferences, so a third goal is to allocate in a way that is truthful (incentivizes people to tell us their true preferences).
Can we achieve all three goals simultaneously? The answer depends on how exactly we define efficiency, fairness and truthfulness. For the most commonly-used definitions, the answer is ‘yes.’ We can use the random serial dictatorship mechanism (also called ‘random priority’): place people in a random order, and one at a time, allow them to choose their favorite object from those that remain.
Are there other ways to achieve these three goals? Many algorithms are known, but surprisingly, almost all of them have been shown to be equivalent to random serial dictatorship. That is, they are different algorithms, but they produce the same distribution over outcomes! This fall, I learned of the paper Strategyproof Stochastic Assignment by Aytek Erdil, which constructs a mechanism which is efficient, fair, truthful, and not equivalent to random serial dictatorship. You can read about the details of this construction in my earlier blog post.
Overview
This post argues that perhaps the research community has been using the wrong definition of truthfulness.
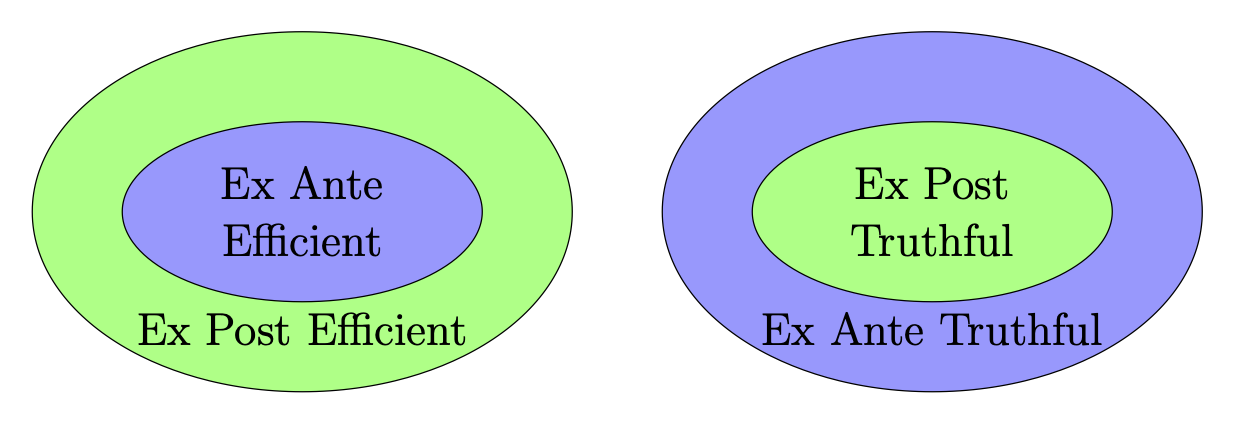
There are two natural approaches to defining what it means for a random mechanism \(M\) to satisfy property \(P\): it can satisfy this property ex post (after the randomness of the mechanism is resolved), or ex ante (before the randomness is resolved). See Decomposing Random Mechanisms by Marek Pycia and Utku Unver for a more general treatment of the relationship between ex ante and ex post properties.
Depending on the property \(P\), the ex ante requirement can be either stronger or weaker than its ex post counterpart. In particular, as I explain below, we have the following relationship.
Erdil’s work proves that there are multiple mechanisms which are ex post efficient, ex ante truthful, and symmetric.
The choice to use ex post efficiency is necessitated by the fact that ex ante efficiency (also named ‘ordinal efficiency’) cannot be achieved at all if we also want truthfulness (either ex ante or ex post) and a weak fairness criteria (equal treatment of equals) – see Theorem 2 of A new solution to the random assignment problem by Bogomolnaia and Moulin.
The choice to use ex ante truthfulness is very standard, going back at least to Bogomolnaia and Moulin (Definition 5). On its own, this definition is very natural, and until recently, I hadn’t questioned it. The more I think about it, however, the more it seems unnatural to use ex ante truthfulness in conjunction with ex post efficiency. This inspires the following question, which to my knowledge is open! Someone should solve it.
Open Problem Is every mechanism that is ex post Pareto efficient, ex post truthful, and symmetric equivalent to random serial dictatorship?
I think this problem hasn’t gotten much attention in part because most papers present only a single definition of efficiency and truthfulness (without labeling these definitions ‘ex post’ or ‘ex ante.’) This makes it unclear that other natural or interesting definitions exist. One goal of this post is to present definitions side by side, to make the choices made by past researchers more apparent.
Definitions
There is a set of agents \(\mathcal{A}\) and a set of objects \(\mathcal{O}\), with \(|\mathcal{O}| \ge |\mathcal{A}|\). (This last assumption isn’t necessary, but slightly simplifies the definitions below.)
Deterministic Allocations and Mechanisms
An allocation is a one-to-one function from \(\mathcal{A}\) to \(\mathcal{O}\).
A preference profile \(\succ\) specifies for each agent \(i\), a strict ordering \(\succ_i\) over objects.
A deterministic mechanism is a function from preference profiles to allocations.
Deterministic mechanism \(M\) is said to be Pareto efficient if for every preference profile \(\succ\), there is no allocation that is as good (according to \(\succ\)) as \(M(\succ)\) for every agent, and strictly better for some agent.
A deterministic mechanism is truthful if, for any preference profile \(\succ\) and agent \(i\), the object that \(i\) receives from reporting \(\succ_i\) is at least as good (according to \(\succ_i\)) as the object that \(i\) receives from reporting any other preference.
Ex Post Efficiency and Truthfulness
In order to achieve fairness, we often use random mechanisms. A random mechanism is a function that maps each preference profile to a distribution over allocations.
One way to construct a random mechanism is to use a lottery over deterministic mechanisms. This suggests the following definitions of efficiency and truthfulness for random mechanisms.
- Random mechanism \(M\) is ex post Pareto efficient if it can be expressed as a lottery over deterministic mechanisms, each of which is Pareto efficient.
- Random mechanism \(M\) is ex post truthful if it can be expressed as a lottery over deterministic mechanisms, each of which is truthful.
These are the definitions that I provide to students who take my class IE 5285, in part because of their simplicity. My use of the phrase “ex post” aligns with the usage in Pycia and Unver, and is intended to reflect the fact that the properties above hold after uncertainty about the mechanism is resolved.
Ex Ante Efficiency and Truthfulness
An alternative approach is to come up with definitions of efficiency and truthfulness that hold ex ante – that is, before resolving the randomness of the mechanism. To define these formally takes a little bit of work. Our definition will borrow from the concept of stochastic dominance of random variables.
Each distribution over allocations induces a (random) outcome for each agent, which specifies the probability with which the agent gets each object. Let \(x\) and \(y\) be two distributions over outcomes, and \(\succ\) a preference profile. Say that agent \(i\) weakly \(\succ\)-prefers \(x\) to \(y\) if for each position \(k\), the probability that agent \(i\) receives a top-\(k\) object (according to \(\succ_i\)) under \(x\) is at least as high the corresponding probability under \(y\). If in addition the probability of receiving a top \(k\) choice is strictly higher under \(x\) for some \(k\), then we say that agent \(i\) strictly \(\succ\)-prefers \(x\) to \(y\).
- Random mechanism \(M\) is ex ante Pareto efficient if for every preference profile \(\succ\), there is no distribution over allocations that is weakly \(\succ\)-preferred by every agent to \(M(\succ)\), and strictly \(\succ\)-preferred by some agent.
- Random mechanism \(M\) is ex ante truthful if for any preference profile \(\succ\), each agent \(i\) weakly \(\succ\)-prefers \(M(\succ)\) to the distribution over outcomes that would result if \(i\) reported any other preference.
These definitions clearly parallel the corresponding definitions for deterministic mechanisms, with stochastic dominance providing the means of comparing two distributions over allocations. They go at least as far back as Bogomolnaia and Moulin (2001), who refer to ex ante efficiency as ‘ordinal efficiency.’ (While they had good reasons for their choice of terminology, I use the phrase ex ante efficiency in this post to highlight the parallel with ex ante truthfulness. Somewhat confusingly, Bogomolnaia and Moulin use ‘ex ante efficiency’ to refer to an even stronger notion considered by Zhou (1990).)
Relationship Between Ex Post and Ex Ante Definitions
It is not a priori clear how these definitions relate to each other. Are they equivalent? Is one stronger than the other?
Ex Post Truthfulness is Stronger than Ex Ante Truthfulness
A brief consideration shows that ex post truthfulness implies ex ante truthfulness. Instead of giving a formal proof, I will note that intuitively, if someone can never benefit from lying even if they know the random seed used by the mechanism, then they certainly cannot benefit if they don’t know that seed. However, the converse does not hold: some ex ante truthful mechanisms cannot be expressed as a lottery over truthful deterministic mechanisms.
The simplest example illustrating this fact comes from Pycia and Unver (2015), Theorem 4. There are three objects, one agent. Mechanism \(M\) gives the agent their first choice half of the time, and their second choice the other half of the time. It is easy to see that this is ex ante truthful: any lie gives the agent a worse lottery over outcomes. However, \(M\) cannot be expressed as a lottery over deterministic truthful mechanisms.
To prove this, suppose that agent reports \(a \succ b \succ c\). Let \(\mathcal{M}_1\) be the set of deterministic mechanisms in the support of \(M\) that give the agent \(a\), and \(M_2\) the set of deterministic mechanisms in the support of \(M\) that give the agent \(b\). We know that \(M\) must choose a mechanism in \(M_1\) half the time, and a mechanism in \(M_2\) the other half of the time.
Now suppose the agent reports \(b \succ c \succ a\). Mechanisms in \(M_2\) must give the agent \(b\), as they are truthful. Since \(M\) gives the agent \(b\) and \(c\) with equal probability, it follows that each mechanism in \(M_1\) must give the agent \(c\).
Now suppose the agent reports \(c \succ a \succ b\). Mechanisms in \(M_1\) must give the agent \(c\), as they are truthful. Since \(M\) gives the agent \(c\) and \(a\) with equal probability, it follows that each mechanism in \(M_2\) must give the agent \(a\). But then mechanisms in \(M_2\) award \(a\) on report \(c \succ a \succ b\) and \(b\) on report \(a \succ b \succ c\), implying that they are not truthful.1
Ex Post Pareto Efficiency is Weaker than Ex Ante Pareto Efficiency
It is easy to see that ex ante efficiency implies ex post efficiency. In particular, a mechanism which is not ex post Pareto efficient cannot be ex ante Pareto efficient: if \(M(\succ)\) places positive probability on an allocation that is not Pareto efficient, then we can \(\succ\)-stochastically dominate \(M(\succ)\) by, for example, running Top Trading Cycles starting from the allocation \(M(\succ)\).
However, it is possible that a mechanism that randomizes over Pareto efficient assignments does not produce a random allocation that is ex ante efficient. This fact was demonstrated by Bogomolnaia and Moulin (2001) using an example with four objects and four agents. Agents 1 and 2 rank \(a \succ b \succ c \succ d\). Agents 3 and 4 rank \(b \succ a \succ d \succ c\).
Intuitively, we should give \(a\) and \(b\) to agents who rank them first, and \(c\) and \(d\) to agents who rank them third. However, random serial dictatorship (which is ex post Pareto efficient) sometimes gives \(a\) or \(b\) to agents who rank them second (and \(c\) or \(d\) to agents who rank them fourth). Specifically, it produces these assignment probabilities:
| a | b | c | d | |
|---|---|---|---|---|
| 1 | 5/12 | 1/12 | 5/12 | 1/12 |
| 2 | 5/12 | 1/12 | 5/12 | 1/12 |
| 3 | 1/12 | 5/12 | 1/12 | 5/12 |
| 4 | 1/12 | 5/12 | 1/12 | 5/12 |
This is dominated by the following assignment probabilities.
| a | b | c | d | |
|---|---|---|---|---|
| 1 | 1/2 | 0 | 1/2 | 0 |
| 2 | 1/2 | 0 | 1/2 | 0 |
| 3 | 0 | 1/2 | 0 | 1/2 |
| 4 | 0 | 1/2 | 0 | 1/2 |
Closing Thoughts
Which definitions are the “right” ones? The answer to this question is often driven by the domain, which can dictate, for example, which notions of fairness are most salient. Other times, the choice between several similar definitions is driven by mathematics. For example, while ex ante efficiency seems appealing, choosing this definition encounters impossibility results that are not encountered if we are willing to accept ex post efficiency.
In this post, I argue for the use of ex post definitions, rather than ex ante. This argument is partly driven a desire for beauty: I really want it to be the case that random serial dictatorship is the only efficient, truthful, and fair mechanism, for suitable definitions of these concepts.
But I also think that ex post definitions are compelling in practice. I’ll let Pycia and Unver make that case for me. They argue that describing random mechanisms as a lottery over deterministic mechanisms can make them more transparent:
Many market design situations require transparency of the mechanism. Randomness of a mechanism is often a source of additional complexity in explaining and educating the agents who will participate in its implementation. Although simple tie-breakers can easily be explained to the participants in certain situations (e.g., in school choice), more complex random mechanism implementation often hinges on the condition that we can implement a deterministic mechanism to represent the random mechanism. For this reason, the market designer may want to resolve the uncertainty regarding the mechanism as soon as possible, before the participants’ private information is collected. Thus, the representability of a random mechanism as a randomization over deterministic mechanisms that also have the same properties could be crucial to the success of the design. -Pycia and Unver (2015)
They also point out the advantage of being able to offer both guarantees:
When a property… holds both ex ante, i.e., before the uncertainty regarding the mechanismis resolved, and ex post, i.e., after this uncertainty is resolved…, the mechanism is more robust and is not affected by the market participants’ access to information regarding the resolution of the uncertainty in the mechanism. For example, if dominant-strategy incentive-compatibility (or strategy-proofness) is decomposable, then it is best for an agent to reveal his preferences truthfully regardless of if all he knows is that a stochastically strategy-proofmechanism will be implemented or if he knows exactly, after the lottery is resolved, which strategyproof deterministic mechanism will be implemented. If such a decomposition goes through, this deterministic mechanism,in many cases,can be explained more transparently to the participants. -Pycia and Unver (2015)
If you’ve made it all the way to the bottom of this post, thank you for your interest! Let me know by leaving a short comment below.
One might be tempted to try a shorter argument along the lines of “giving an agent their second choice cannot be made truthful”, but this is an oversimplification. In fact, the mechanism \(M_p\) that gives the agent their first choice with probability \(p\) and their second choice with probability \(1-p\) is expressible as a lottery over deterministic truthful mechanisms whenever \(p \ge 2/3\). (Can you see how to do it?)↩︎